11
Perímetres i àrees de polígons
228
7.
ÀREA DE POLÍGONS REGULARS
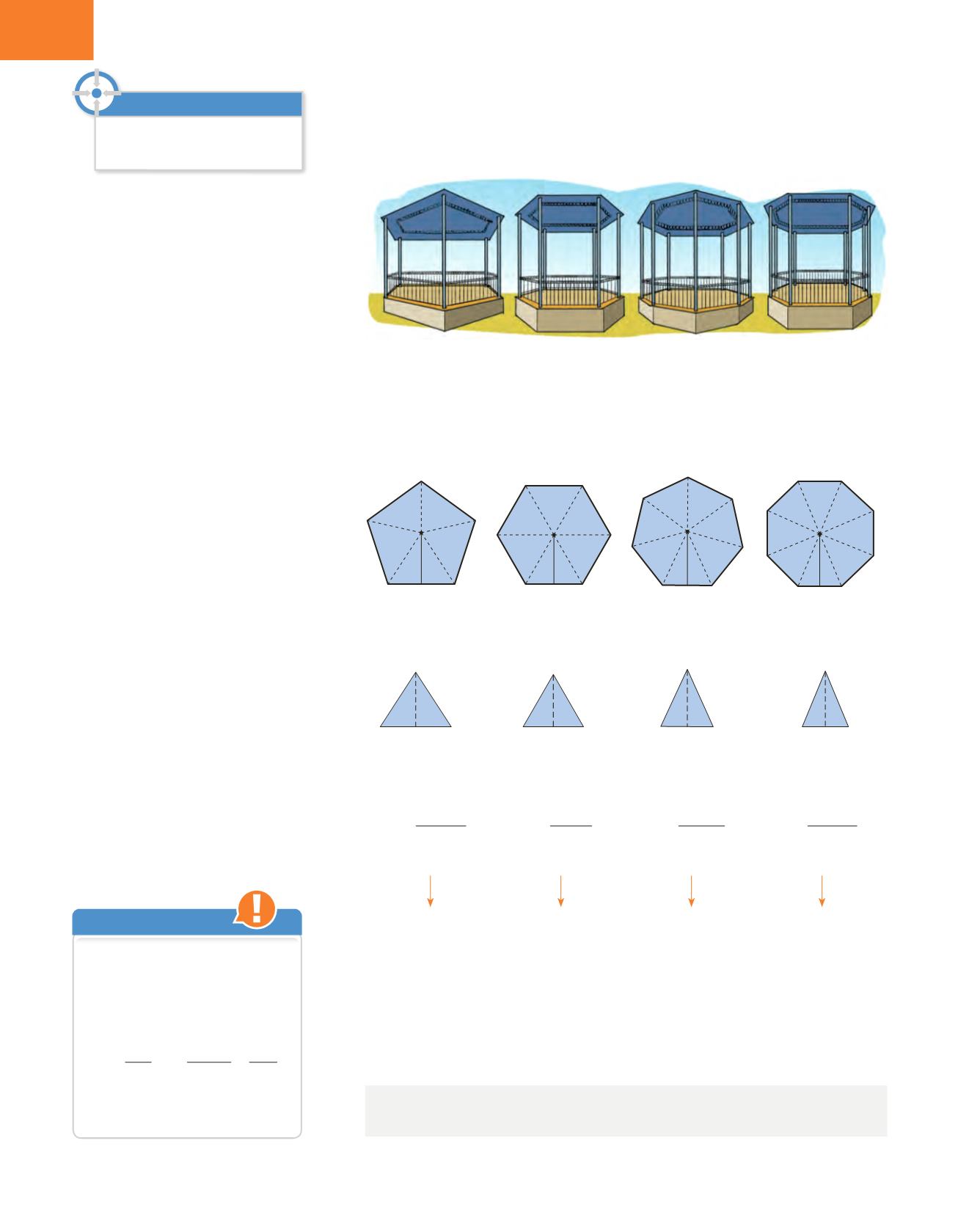
Al parc d’un poble volen instal·lar un templet perquè la banda de música hi puga
fer concerts.
Els tècnics de l’Ajuntament han elaborat diversos projectes diferents basats en
polígons regulars els costats dels quals mesuren 3 m. Només disposen d’un espai
de 40 m
2
i volen triar el templet que tinga la superfície més gran.
Podem descompondre cada polígon regular en tants triangles iguals com costats
tinga el polígon.
3 m
3 m
3 m
3 m
2,06 m
2,6 m
3,11 m
3,62 m
La base de cada triangle coincideix amb el costat del polígon, i l’altura, amb
l’apotema.
3 m
3 m
3 m
3 m
2,06 m
2,6 m
3,11 m
3,62 m
Calculem l’àrea d’un d’aquests triangles i la multipliquem pel nombre de costats
del polígon.
=
=
=
A
A
3 2,06
2
3,09 m
T
T
2
⋅
=
=
=
A
A
3 2,6
2
3,9 m
T
T
2
⋅
=
=
=
A
A
3 3,11
2
4,665 m
T
T
2
⋅
=
=
=
A
A
3 3,62
2
5,43 m
T
T
2
⋅
Àrea del
pentàgon
Àrea de
l’hexàgon
Àrea de
l’heptàgon
Àrea de
l’octàgon
A
=
5
⋅
3,09
=
A
=
15,45 m
2
A
=
6
⋅
3,9
=
A
=
23,4 m
2
A
=
7
⋅
4,665
=
A
=
32,655 m
2
A
=
8
⋅
5,43
=
A
=
43,44 m
2
En comparar les àrees obtingudes, decideixen instal·lar-lo en forma
d’heptàgon, ja que no disposen de superfície suficient per a alçar-lo en forma
d’octàgon.
L’
àrea d’un polígon regular
és igual al seu costat per la seua apotema
dividida per dos i multiplicada pel nombre de costats
.
Aprendràs a...
❚●
Calcular l’àrea d’un polígon
regular.
Para atenció
Com que en un polígon regular
el perímetre és igual al nombre
de costats per la longitud del
costat, la fórmula de la seua
àrea també és:
A
c a
n
c n a P a
2
2
2
⋅
⋅
⋅ ⋅
⋅
=
=
=
On
P
és el perímetre, i
a,
l’apotema.


