69
4
Activitats
Copia en el quadern i aparella les equacions amb les
solucions corresponents.
10
Calcula el valor de
m
en l’equació de segon grau
x
2
+
mx
−
24
=
0, si
x
=
3 n’és una de les solucions.
Resol aquestes equacions de segon grau.
a)
x
2
−
3
x
−
10
=
0
c)
2
x
2
−
6
x
+
4
=
0
b)
x
2
+
x
−
12
=
0
d)
x
2
+
x
−
42
=
0
Indica el nombre de solucions de les equacions de
segon grau, sense resoldre-les.
a)
x
2
−
6
x
+
9
=
0
c)
4
x
2
−
4
x
+
1
=
0
b)
x
2
+
x
+
1
=
0
d)
x
2
−
5
x
+
6
=
0
Escriu una equació de segon grau les solucions de la
qual siguen 4 i 5.
Determina els valors de
a
perquè
x
2
+
ax
+
4
=
0 tinga
una única solució.
11
12
13
14
15
Calcula el valor dels coeficients
b
i
c
de l’equació
3
x
2
+
bx
+
c
=
0, si 2 i
−
3 en són les solucions.
16
Resol, sense fer els productes, aquestes equacions de
segon grau.
a)
(
x
+
1)(
x
−
1)
=
0
c)
3(
x
−
4)(
x
+
4)
=
0
b)
(2
x
+
3)(2
x
−
3)
=
0
d)
(4
x
−
5)(4
x
+
5)
=
0
Si la suma d’un nombre positiu i el seu quadrat és
756, de quin nombre es tracta?
17
18
Calcula el perímetre d’un quadrat, si sabem que,
en augmentar la longitud de dos costats paral·lels
12 cm, obtenim un rectangle que té una superfície
de 364 cm
2
.
19
``
Calcula l’equació de segon grau el coeficient
principal de la qual és 2, si sabem que les solucions
són 1 i
−
3.
Solució
Si el coeficient principal és 2, aleshores l’equació és de
la forma:
2
x
2
+
bx
+
c
=
0
Com que les solucions de l’equació de segon grau
coincideixen amb les arrels del polinomi amb el mateix
grau:
2
x
2
+
bx
+
c
=
2(
x
−
1)(
x
+
3)
=
2
x
2
+
4
x
−
6
Així, l’equació és:
2
x
2
+
4
x
−
6
=
0
EXERCICI RESOLT
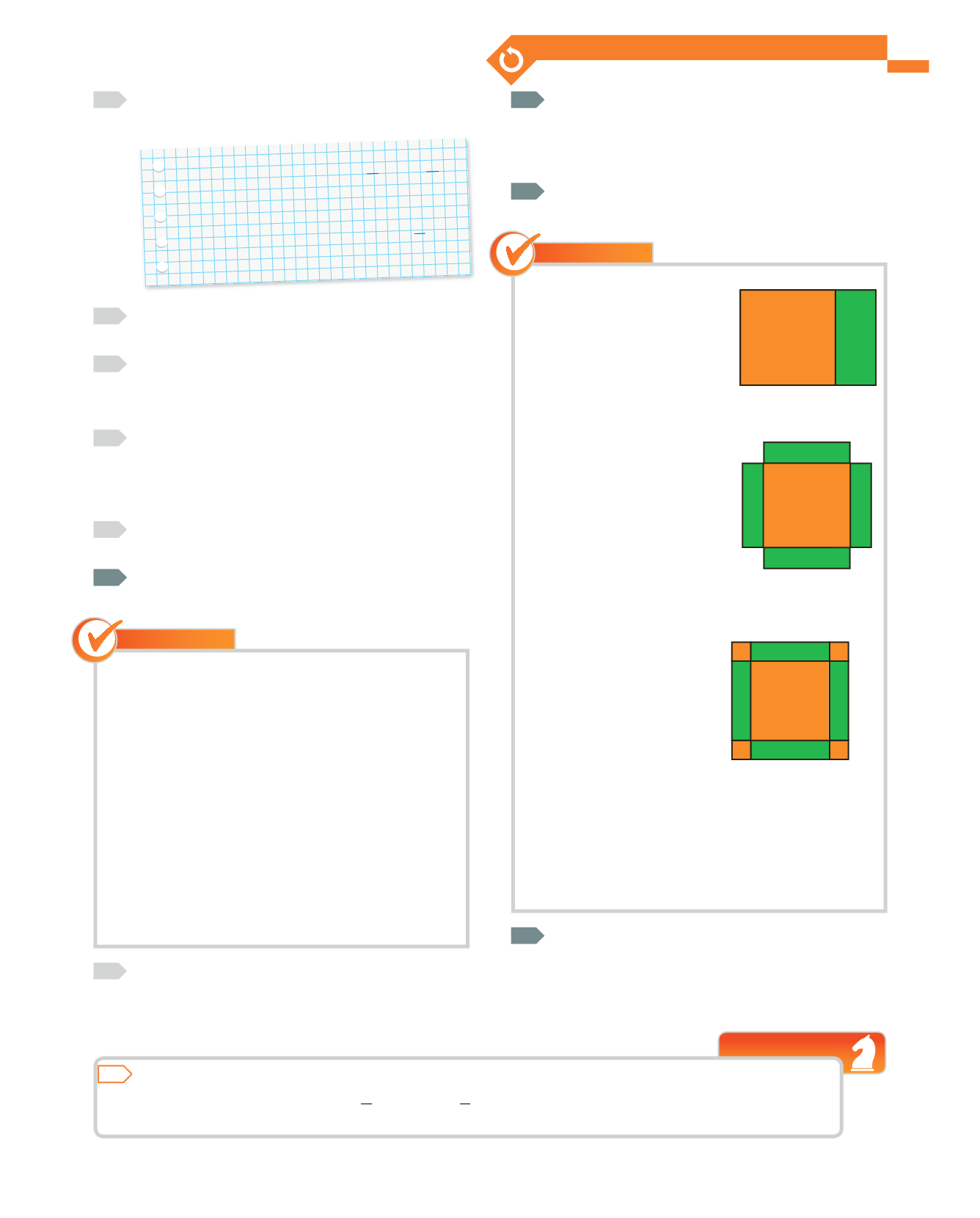
``
En augmentar 4 m dos
costats paral·lels d’un
quadrat, obtenim un
rectangle de 96 m
2
d’àrea. Quina longitud
té el costat del quadrat
original?
Solució
Anomenem
x
la longitud
del costat del quadrat i
dibuixem sobre cadascun
dels costats un rectangle els
costats del qual siguen
x
i 1,
respectivament.
L’àrea de la figura que obtenim mesura:
x
2
+
4
x
=
96
→
x
(
x
+
4)
=
96
Afegim quatre quadrats als
cantons, de manera que
completem una nova figura,
un quadrat de costat
x
+
2,
la superfície del qual mesura:
96
+
4
=
100 m
2
Aleshores: (
x
+
2)
2
=
100
Resolem:
x
+
2
= ±
10
→
x
1
=
10
−
2
=
8
x
2
=
−
10
−
2
=
−
12
⎧
⎨
⎪⎪
⎩⎪⎪
Com que la mesura del costat del quadrat no pot ser un
valor negatiu, la solució del problema és 8 m.
EXERCICI RESOLT
x
4
x
x
x
1
1
1
1
x
+2
x
+2
DESAFIAMENT
Comprova que, si
x
1
i
x
2
són les solucions d’una equació de segon grau
ax
2
+
bx
+
c
=
0, es verifiquen les
relacions de Cardano:
x
1
+
x
2
=
−
b
a
y
x
1
⋅
x
2
=
c
a
i
x
1
+
x
2
=
−
b
a
y
x
1
⋅
x
2
=
c
a
20
2x
2
+
3x
−
2
=
0
x
2
−
5x
+
6
=
0
x
2
−
2x
−
120
=
0
6x
2
+
17x
+
12
=
0
x
=
−
3
2 y x
=
−
4
3
x
=
−
10 y x
=
12
x
=
−
2 y x
=
1
2
x
=
2 y x
=
3


