180
¿QUÉ
10
tienes que saber
?
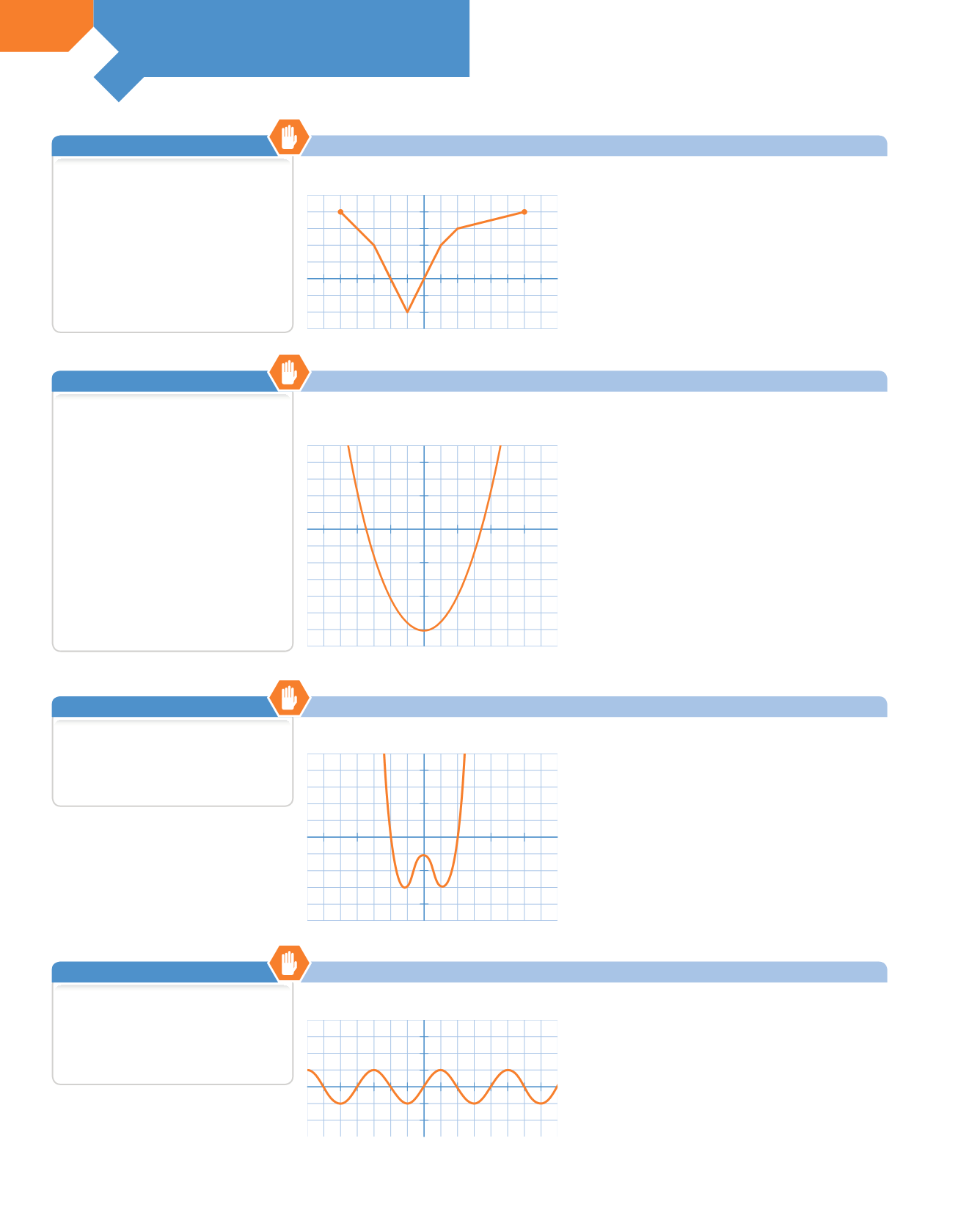
Determina el dominio, el recorrido y los puntos de corte de esta función.
Dominio: [
−
5, 6]
Recorrido: [
−
2, 4]
Puntos de corte:
❚
Con el eje
X:
(
−
2, 0) y (0, 0)
❚
Con el eje
Y:
(0, 0)
Dominio, recorrido y puntos de corte
Ten en cuenta
❚❚
El
dominio
es el conjunto de
los valores que puede tomar la
variable independiente
x.
❚❚
El
recorrido
es el conjunto de
los valores que toma la variable
dependiente
y.
❚❚
Los
puntos de corte
con los ejes
son de la forma:
(
x
, 0) (0,
y
)
O
1
1
X
Y
Indica si la función
f
(
x
)
=
x
2
−
3 es continua y determina los intervalos de crecimiento
y decrecimiento, así como los máximos y los mínimos, si los tiene.
Continuidad:
La función es continua en todo su dominio.
Monotonía:
Es creciente en el intervalo (0,
+
∞
).
Es decreciente en el intervalo (
−∞
, 0).
La función tiene un mínimo en (0,
−
3).
No tiene máximos.
Continuidad y monotonía
Ten en cuenta
❚❚
Una función es
continua
en un
intervalo si no tiene saltos.
❚❚
Una función es
creciente
si, cuando
aumenta la variable
x,
también
aumenta la variable
y.
❚❚
Una función es
decreciente
si,
cuando aumenta la variable
x,
la
variable
y
disminuye.
❚❚
Un punto es un
máximo
si en él la
función cambia de ser creciente a
ser decreciente.
❚❚
Un punto es un
mínimo
si en él la
función pasa de ser decreciente a
ser creciente.
O
1
1
X
Y
¿Es periódica la función representada en esta gráfica?
La función es periódica.
Su período es
T
=
4.
Funciones periódicas
Ten en cuenta
❚❚
Una función es
periódica
de período
T
cuando el
comportamiento de la función
en un intervalo se repite en
intervalos sucesivos.
O
1
1
X
Y
¿Es simétrica la función
f
(
x
)
=
3
x
4
−
4
x
2
?
Para estudiar la simetría de
f
(
x
)
=
3
x
4
−
4
x
2
hay
que calcular
f
(
−
x
):
f
(
−
x
)
=
3(
−
x
)
4
−
4(
−
x
)
2
=
3
x
4
−
4
x
2
=
f
(
x
)
Se trata de una función par,
es simétrica respecto del eje de ordenadas,
porque cumple que:
f
(
−
x
)
=
f
(
x
)
Funciones simétricas
Ten en cuenta
❚❚
Función par
f
(
−
x
)
=
f
(
x
)
❚❚
Función impar
f
(
−
x
)
=
−
f
(
x
)
O
1
1
X
Y


