186
10
Funciones
La
tasa de variación
de una función continua en un intervalo [
a, b
] es el valor:
TV
[
a, b
]
=
f
(
b
)
−
f
(
a
)
La tasa de variación nos informa de cómo varía la función en ese intervalo y se escribe:
TV
[
a, b
]
=
f
(
b
)
−
f
(
a
)
AVANZA
A1.
Halla la tasa de variación en el intervalo [1, 3] de
la función
f
(
x
)
=
2
x
−
1. ¿Cómo es la función en
este intervalo: creciente o decreciente?
A2.
Determina la tasa de variación de la función
f
(
x
)
=
2
−
x
en el intervalo [
−
2,
−
1]. Razona
cómo es la función en este intervalo: creciente o
decreciente.
A3.
Calcula la tasa de variación en el intervalo [
−
1, 3]
de las funciones que se presentan a continuación.
a)
f
(
x
)
=
x
+
2
b)
f
(
x
)
=
−
x
2
−
4
x
−
2
c)
f
(
x
)
=
2
¿Hay alguna que sea decreciente?
FUNCIONES EN LOS MEDIOS DE COMUNICACIÓN
Tasa de variación de una función en un intervalo
Un hecho de trascendencia para la
historia es la gran crisis económica y
mundial que se desató en el año 2008.
En todas las funciones relacionadas
con el consumo de bienes y servicios, la
actividad laboral, los servicios sociales,
etc., destacan las cifras de ese año.
El coche ha sido siempre el artículo
de consumo por excelencia. La gráfica
representa las cifras de ventas de
coches en España entre los años 1997
y 2012, en miles de unidades. Observa
que en el año 2008 hubo una caída
en las ventas con respecto al año
anterior.
F1.
Fíjate en la gráfica y responde: ¿Cuántos coches se
vendieron en los años 2003 y 2004? ¿En qué períodos
hubo un aumento de las ventas?
F2.
Elabora un informe sobre las ventas de coches en
España entre los años 2000 y 2010 indicando en qué
intervalos se produjeron mayores variaciones.
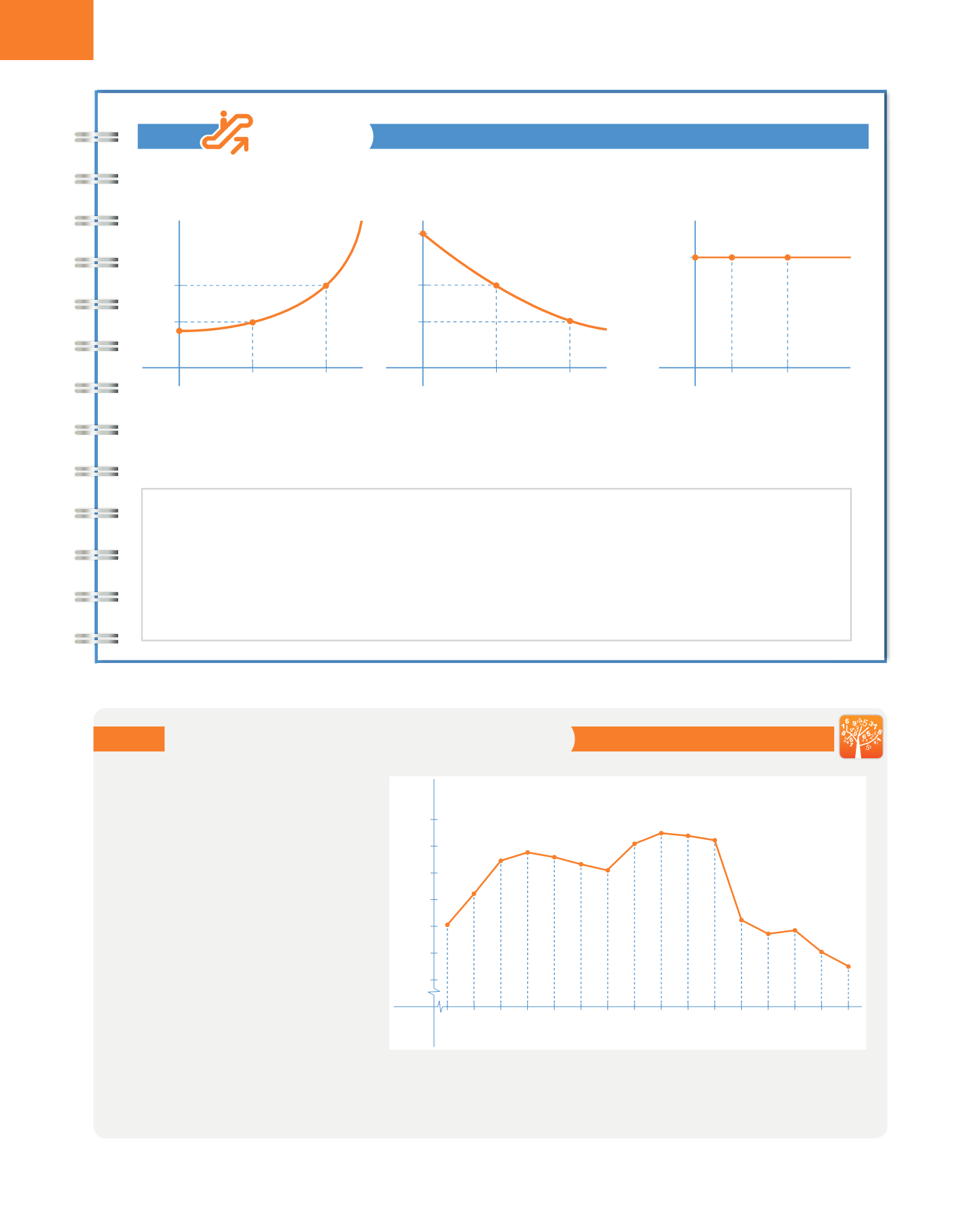
Si la función es creciente:
f
(
b
)
−
f
(
a
) > 0
TV
[
a, b
] > 0
Si la función es decreciente:
f
(
b
)
−
f
(
a
) < 0
TV
[
a, b
] < 0
Si la función es constante:
f
(
b
)
−
f
(
a
)
=
0
TV
[
a, b
]
=
0
O
a
b
f
(
a
)
f
(
b
)
X
Y
1073
O
1997
600
2008
X
Y
1263
1498
1565 1509
1489 1464
1612
1648 1635 1615
1161
955 985
811
700
O
a
b
f
(
b
)
f
(
a
)
X
Y
O a
b
f
(
a
) =
f
(
b
)
X
Y


