107
4
Estructura atómica y molecular
1.
Describe el modelo atómico de Bohr indicando las ca-
racterísticas que conserva con respecto al modelo de
Rutherford y las aportaciones específicas que realizó
Bohr.
El modelo de Rutherford entraba en contradicción con las
ecuaciones de Maxwell que predecían que una carga eléctri-
ca acelerada debía emitir energía en forma de radiación elec-
tromagnética, de esta forma el electrón tendría que acabar
estrellado contra el núcleo. Tampoco explicaba los espectros
atómicos de los gases a baja presión. Bohr solucionó estas
cuestiones enunciando tres postulados:
1. Los electrones giran en torno al núcleo solo en ciertas
órbitas circulares estables donde al moverse no irradian
energía (órbitas estacionarias).
2. De todas las órbitas que cumplen que
F
eléctrica
=
F
centrípeta
solo están permitidas aquellas cuya energía adopte unos
valores, y no otros, determinados por un número cuántico
n
(
n
=
1, 2, 3…).
3. Un electrón solo emite radiación cuando salta de una ór-
bita permitida de mayor energía a otra de menor energía,
y la absorbe cuando salta de una de menor a otra de ma-
yor energía. En ambos tránsitos emite o absorbe un fotón
cuya energía es la diferencia de energía entre ambos nive-
les (
E
=
E
2
−
E
1
=
h
υ
).
2.
Indica el número de protones, neutrones y electrones
existentes en:
120
50
Sn
2
+
,
16
32
S
2
−
;
19
39
K.
❚
120
50
Sn
2
+
: n.º de protones
=
50; n.º de neutrones
=
70; n.º de
electrones
=
48
❚
32
16
S
2
−
: n.º de protones
=
16; n.º de neutrones
=
16; n.º de
electrones
=
18
❚
39
19
K: n.º de protones
=
19; n.º de neutrones
=
20; n.º de
electrones
=
19
3.
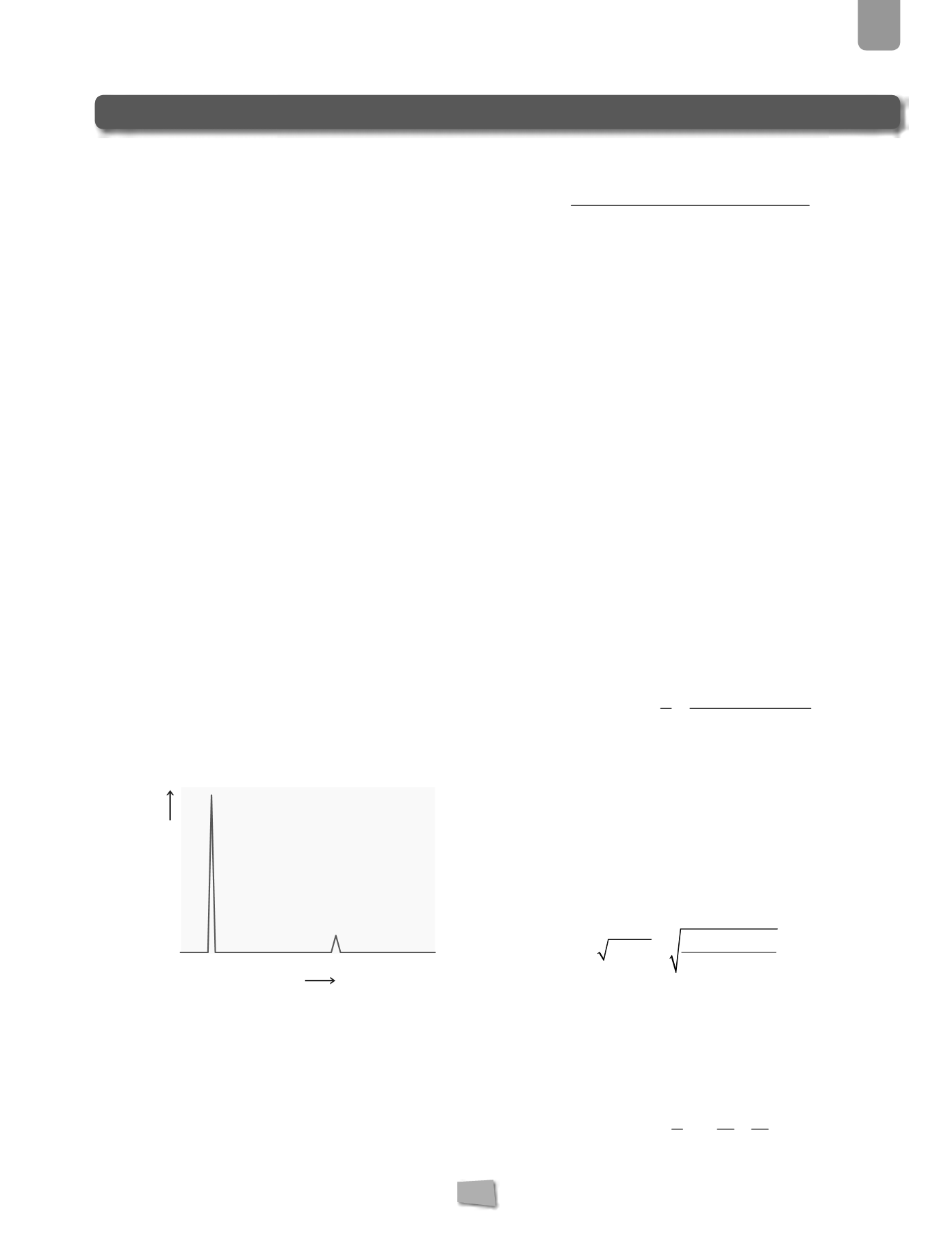
Calcula la masa atómica del carbono a partir de los da-
tos de la figura.
12,00000
13,00335
0,011
0,989
Masa
Abundancia relativa
Masa atómica del C
=
0,989
⋅
12,00000 u
+
+
0,011
⋅
13,00335 u
=
11,868
+
0,143
=
12,011 u
4.
La masa atómica del oxígeno es 15,99937. Sabiendo
que el oxígeno tiene tres isótopos:
16
8
O, con masa ató-
mica 15,99491 u y abundancia 99,75%,
17
8
O, con masa
atómica 16,99914 u y abundancia 0,037%; y
18
8
O, ¿cuál
es la masa atómica del tercer isótopo?
Masa atómica del O
=
15,99937 u
=
0,9975
⋅
15,99491 u
+
0,00037
⋅
16,99914 u
+
0,00204
⋅
x
x
=
masa atómica
1
8
18
O
=
=
[15,99937 u
−
(15,95636
+
0,00629)]
0,00204
=
18,00000
5.
Dos propiedades del
39
K son: reacciona violentamen-
te con el agua desprendiendo dihidrógeno y tiene una
masa de 38,9637 u. ¿Cuál de esas dos propiedades será
válida también para el
40
K?
Solo la primera ya que el
39
K y el
40
K son isótopos, por tanto
son átomos del mismo elemento y como consecuencia ten-
drán las mismas propiedades químicas pero diferente masa.
6.
Explica la diferencia entre los espectros atómicos de
emisión y los de absorción.
El
espectro de emisión
es el conjunto de rayas o líneas colo-
readas separadas por espacios oscuros (en la zona del visible),
que aparecen cuando una sustancia es calentada hasta la
incandescencia y su luz se hace pasar a través de un prisma
óptico o rejilla de difracción. Mientras que el
espectro de
absorción
es el conjunto de rayas negras que deja una sus-
tancia sobre una banda coloreada (en la zona del visible) des-
pués de absorber la radiación proporcionada por una fuente
luminosa externa.
7.
Calcula la velocidad del electrón emitido por el átomo
de Cs al iluminarlo con una radiación de
λ
=
600 nm.
Datos:
h
=
6,63
⋅
10
−
34
J s;
c
=
3
⋅
10
8
m s
−
1
;
m
e
−
=
9,107
⋅
10
−
31
kg;
W
extracción del Cs
=
3,2
⋅
10
−
19
J
Transformamos 600 nm a metros: 6
⋅
10
−
7
m
Calculamos la frecuencia de la luz incidente:
υ
=
c
λ
=
3
⋅
10
8
m s
−
1
⋅
10
−
7
m
5
⋅
10
14
s
−
1
Aplicamos la ecuación del efecto fotoeléctrico:
h
υ
=
W
extracción
+
E
c
Sustituimos:
6,63
⋅
10
−
34
J s
⋅
5
⋅
10
14
s
−
1
=
3,2
⋅
10
−
19
J
+
E
c
3,3
⋅
10
−
19
J
=
3,2
⋅
10
−
19
J
+
E
c
Despejamos:
E
c
=
0,1
⋅
10
−
19
J
Como
E
c
=
½
mv
2
, entonces:
v
=
2
E
c
/
m
=
2
⋅
1
⋅
10
−
20
J
9,107
⋅
10
−
31
kg
=
1, 49
⋅
10
5
m/s
8.
Calcula la longitud de onda, la frecuencia, el número de
onda y la energía de la radiación emitida por un elec-
trón situado en el nivel
n
=
2 al caer al nivel
n
=
1.
Dato:
R
=
109677,6 cm
−
1
Para el cálculo de la longitud de onda, aplicamos la ecuación
de Rydberg:
1
λ
=
R
1
n
1
2
−
1
n
2
2
⎛
⎝
⎜⎜⎜⎜
⎞
⎠
⎟⎟⎟⎟⎟
SOLUCIONES DE LA EVALUACIÓN
(página 109)


