Profesor - page 21

105
4
Estructura atómica y molecular
32 Calcula la energía del fotón correspondiente a una ra-
diación de frecuencia 6 ⋅ 10 14 s−1. Determina la longitud
de onda de esa radiación.
Aplicamos la ecuación para hallar el cuanto de energía:
E = h υ= 6,63 ⋅ 10 −34 J s ⋅ 6 ⋅ 1014 s−1 = 3,97 ⋅ 10− 10 J
Calculamos la longitud de onda:
λ = c
υ
= 3 ⋅ 108 m s−1
6 ⋅1014 s−1 = 5 ⋅ 10−7 m = 500 m
33 Los rayos X tienen una longitud de onda que oscila en-
tre 10− 3 nm y 10 nm. Halla la energía correspondiente
e intenta averiguar por qué se llama penetrantes a los
primeros y blandos a los segundos.
Aplicamos la ecuación que permite calcular el cuanto de
energía:
E1 = hc
λ
= 6,63 ⋅ 10−34 J s ⋅ 3 ⋅10 8 m s−1
10− 3 nm ⋅ 10−9 m/nm
= 1,99 ⋅ 10−13 J
Aplicamos de nuevo la ecuación anterior para el otro valor de
la banda:
E2 = hc
λ
= 6,63 ⋅10−34 J s ⋅ 3 ⋅ 108 m s−1
10 nm ⋅10− 9 m/nm
= 1,99 ⋅10−17 J
Estos últimos son menos energéticos que los anteriores (se
los denomina blandos).
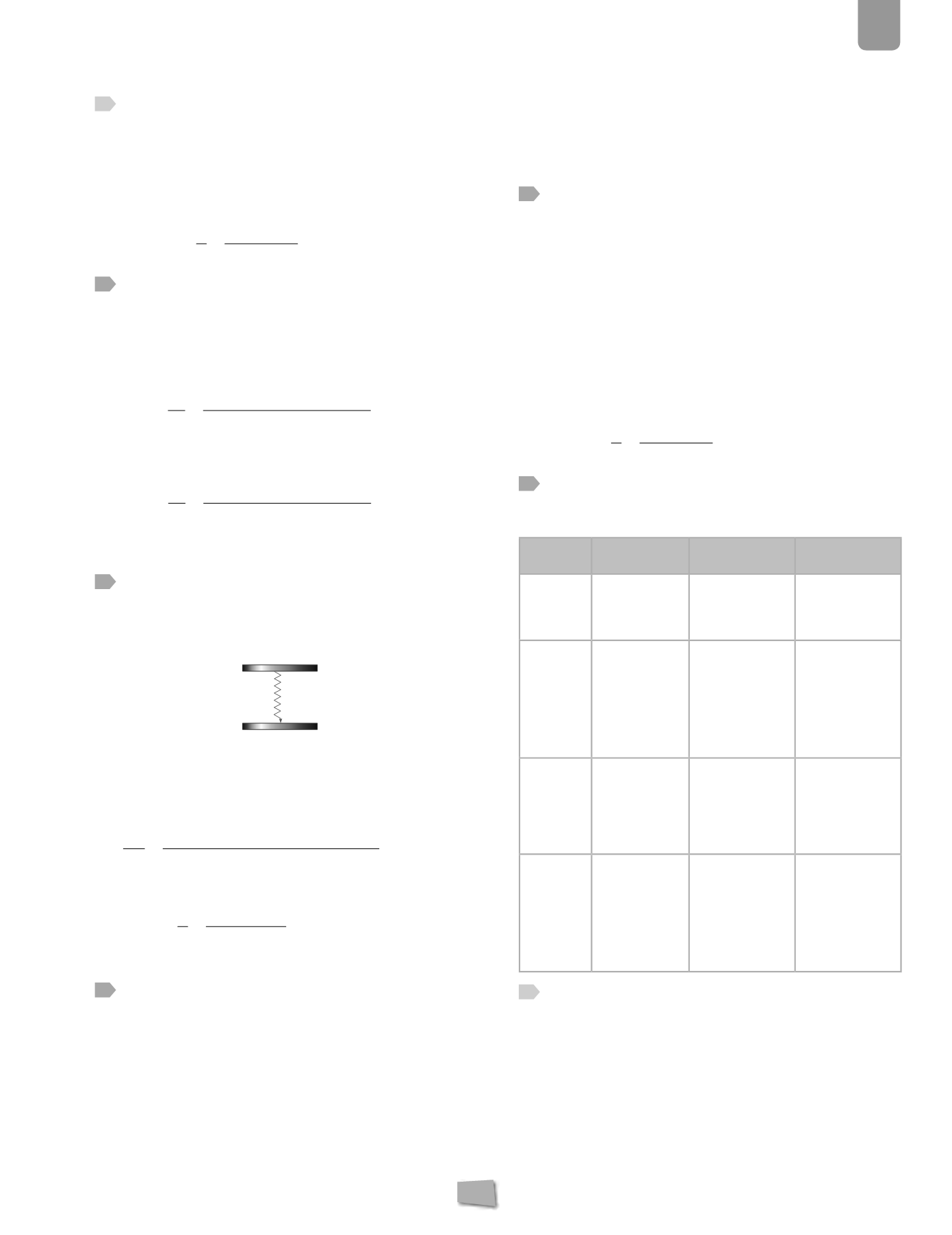
34 Calcula la frecuencia de la radiación electromagnética
que emite un electrón cuando realiza en un átomo el
salto mostrado en la figura. ¿En qué parte del espectro
electromagnético dejará marca?
14,45 eV
e−
10,22 eV
Aplicamos la ecuación que permite hallar la variación de
energía correspondiente a un salto electrónico:
E = h υ
Despejando la frecuencia y sustituyendo los datos:
υ = ΔE
h
= (14, 45 − 10,22) eV ⋅ 1,6 ⋅10−19 J/eV
6,63 ⋅ 10−34 J s
= 1,02 ⋅1015 s−1
Calculamos la longitud de onda:
λ = c
υ
= 3 ⋅10 8 m s−1
1,02 ⋅1015 s−1 = 2,94 ⋅10 −7 m = 294 nm
Pertenece a la región del ultravioleta.
35 Calcula la frecuencia y longitud de onda del fotón emi-
tido por el tránsito del electrón del átomo de hidróge-
no del nivel 3 al nivel 2, sabiendo que entre ellos hay
una diferencia de energía de 1,89 eV.
Dato: 1 eV =1,6 ⋅ 10−19 J
La diferencia de energía en julios será:
1,89 eV ⋅ 1,6 ⋅ 10− 19 J/1 eV = 3,02 ⋅ 10 −19 J
La energía del fotón emitido coincide con esta diferencia de
energía entre niveles. Puesto que E = h υy λ υ= c:
υ= E/h = 3,02 ⋅ 10 −19 J/6,63 ⋅ 10 −34 J s = 4,56 ⋅ 1014 s−1
λ = c/ υ= 3 ⋅ 10 8 m s−1/4,56 ⋅ 10 14 s−1 = 6,58 ⋅ 10 −7 m
La frecuencia cae dentro del rango del visible, entre el Ama-
rillo y el rojo.
36 Calcula la longitud de onda (en nm) que debe tener
una luz para que, al iluminar con ella una placa de me-
tal, esta emita electrones a una velocidad de 6,83 ⋅ 105
m/s. Datos: me = 9,1 ⋅ 10−31 kg; υ0 metal = 8 ⋅ 1013 s− 1.
Aplicamos la ecuación del efecto fotoeléctrico:
h υ= h υ0 + ½ mv2
Sustituimos:
6,63 ⋅ 10− 34 J s ⋅ υ= 6,63 ⋅ 10−34 J s ⋅ 8 ⋅ 1013 s− 1 +
+ ½ ⋅ 9,1 ⋅ 10−31 kg ⋅ (6,83 ⋅10 5 m/s) 2
Despejamos υ: υ= 4 ⋅ 1014 s− 1, que transformada a longitud
de onda:
λ = c
υ
= 3 ⋅108 m s− 1
4 ⋅1014 s− 1 = 7,5 ⋅10− 7 m = 750 nm
37 Realiza un resumen de los distintos modelos atómicos
(ideas introducidas, hechos que explica y hechos que no
explica).
Modelo Ideas
introductorias
Hechos que
explican
Hechos que
no explican
De
Thomson
El átomo
contiene
electrones.
La naturaleza
de los rayos
catódicos.
La existencia de
otras partículas.
Los espectros
atómicos.
De
Rutherford
Un núcleo en el
átomo, donde
se encuentran
los protones.
La gran fuerza
de desviación
de una pequeña
región del
átomo al incidir
partículas α.
Que los
electrones se
puedan mantener
girando alrededor
del núcleo.
Los espectros
atómicos
De Bohr Los electrones
solo pueden
encontrarse en
determinadas
zonas del
átomo.
Los espectros
atómicos.
La estructura
fina del espectro
y la naturaleza
ondulatoria de
los electrones.
De los
orbitales
Naturaleza
ondulatoria de
los electrones.
Factores de
probabilidad.
El principio de
Heisenberg y
la naturaleza
ondulatoria de
los electrones.
¿Por qué hay
tantas partículas
elementales?
¿Qué
partículas son
auténticamente
elementales?
38 ¿Cuál es la diferencia entre órbita y orbital?
La órbita es aquella región circular donde unas partículas,
llamadas electrones, giraban a unas ciertas distancias del nú-
cleo. Las distancias de las órbitas al núcleo podían ser medi-
bles con precisión. Sin embargo, la naturaleza ondulatoria
del electrón y el principio de incertidumbre de Heisenberg
obligan a hablar de densidad de carga negativa en el átomo.
Por otro lado, un orbital es la región del espacio en la que
hay una alta probabilidad (entre el 90% y el 99%) de encon-
trar un electrón de determinada energía.