70
Área de polígonos regulares
Perímetros y áreas de polígonos
.
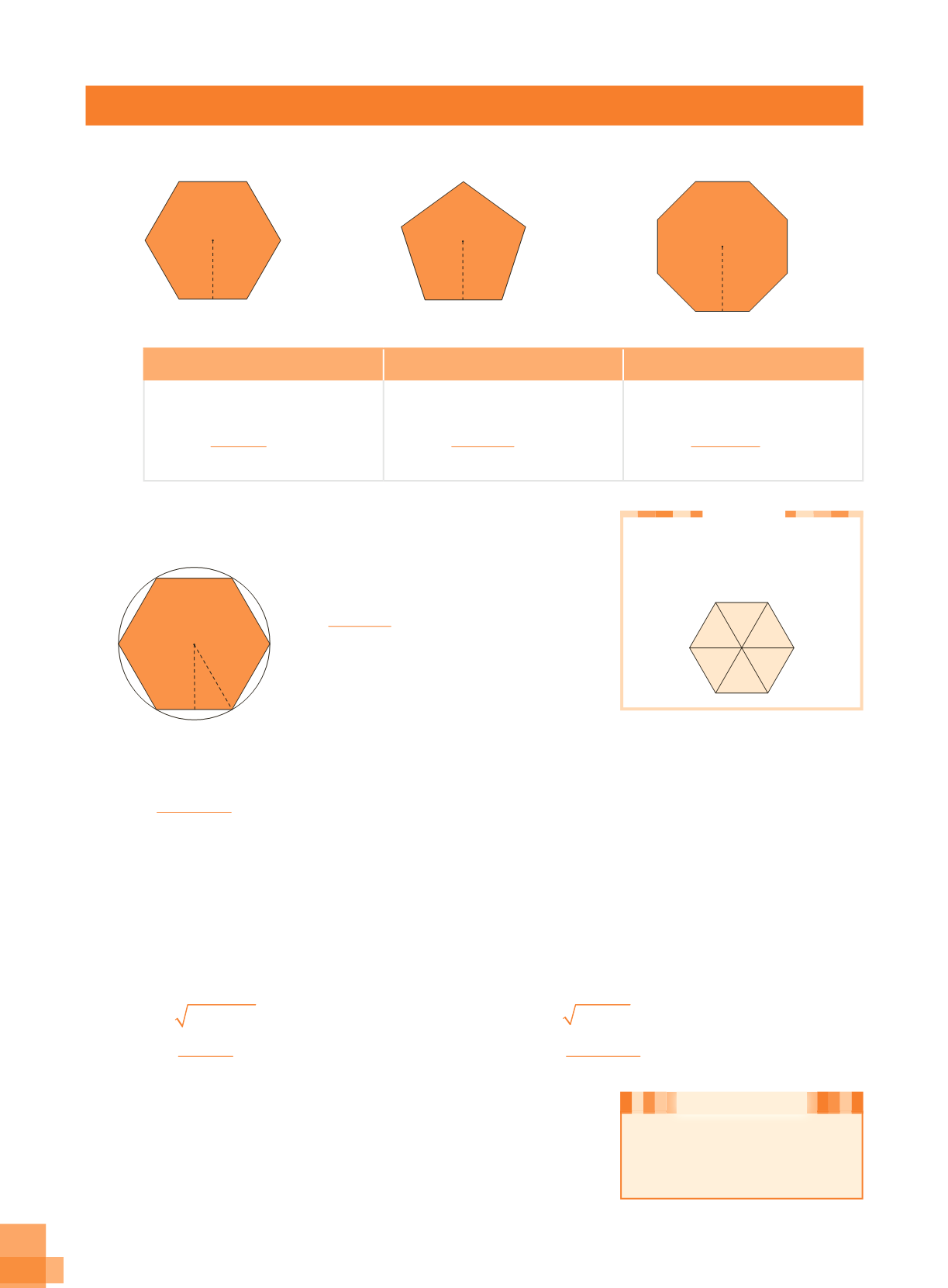
Calcula el perímetro y el área de los siguientes polígonos regulares.
a)
b)
c)
6 cm
5,2 cm
14 cm
9,6 cm
20 cm
24,1 cm
Hexágono regular
Pentágono regular
Octógono regular
P
=
A
=
P
=
A
=
P
=
A
=
.
Un hexágono regular está inscrito en una circunferencia de
12 cm de radio. Calcula su perímetro y su área, sabiendo que
su apotema mide 10,4 cm.
10,4 cm
12 cm
.
La base de una fuente es un polígono regular que tiene 33 m
2
. La distancia del centro de la fuente
a cada uno de los lados es de 2,75 m, y cada lado mide 4 m. ¿Qué forma tiene la fuente?
.
Calcula el área de las siguientes figuras planas.
a)
Un triángulo equilátero de 5 cm de lado.
b)
Un hexágono regular cuyo lado mide 8 cm.
Un hexágono regular se
descompone en 6 triángulos
equiláteros.
Recuerda
Utiliza la calculadora para obtener
la raíz cuadrada de los números que
necesites.
Presta atención
20
⋅
8
=
160 cm
20
⋅
8
⋅
24,1
2
=
1928 cm
2
6
⋅
6
=
36 cm
6
⋅
6
⋅
5,2
2
=
93,6 cm
2
14
⋅
5
=
70 cm
14
⋅
5
⋅
9,6
2
=
336 cm
2
P
=
12
⋅
6
=
72 cm
A
=
72
⋅
10, 4
2
=
374, 4 cm
2
33
=
4
⋅
n
⋅
2,75
2
→
66
=
11
n
→
n
=
6
El polígono tiene 6 lados; por tanto, la fuente es un hexágono regular.
Hallamos la altura del triángulo utilizando
el teorema de Pitágoras.
h
=
5
2
−
2,5
2
=
4,33 cm
A
=
5
⋅
4,33
2
=
10,83 cm
2
Hallamos la apotema del hexágono utilizando
el teorema de Pitágoras.
h
=
8
2
−
4
2
=
6,93 cm
A
=
6
⋅
8
⋅
6,93
2
=
166,32 cm
2


