ACTIVIDADES DE AMPLIACIÓN
8
Restricción del dominio de
f
para que exista
f
–1
Restringir el dominio de
f
(
x
)
x
2
2
x
para que admita función inversa respecto de la composición y obtener su
expresión
f
1
(
x
).
La función
f
(
x
)
�
x
2
�
2
x
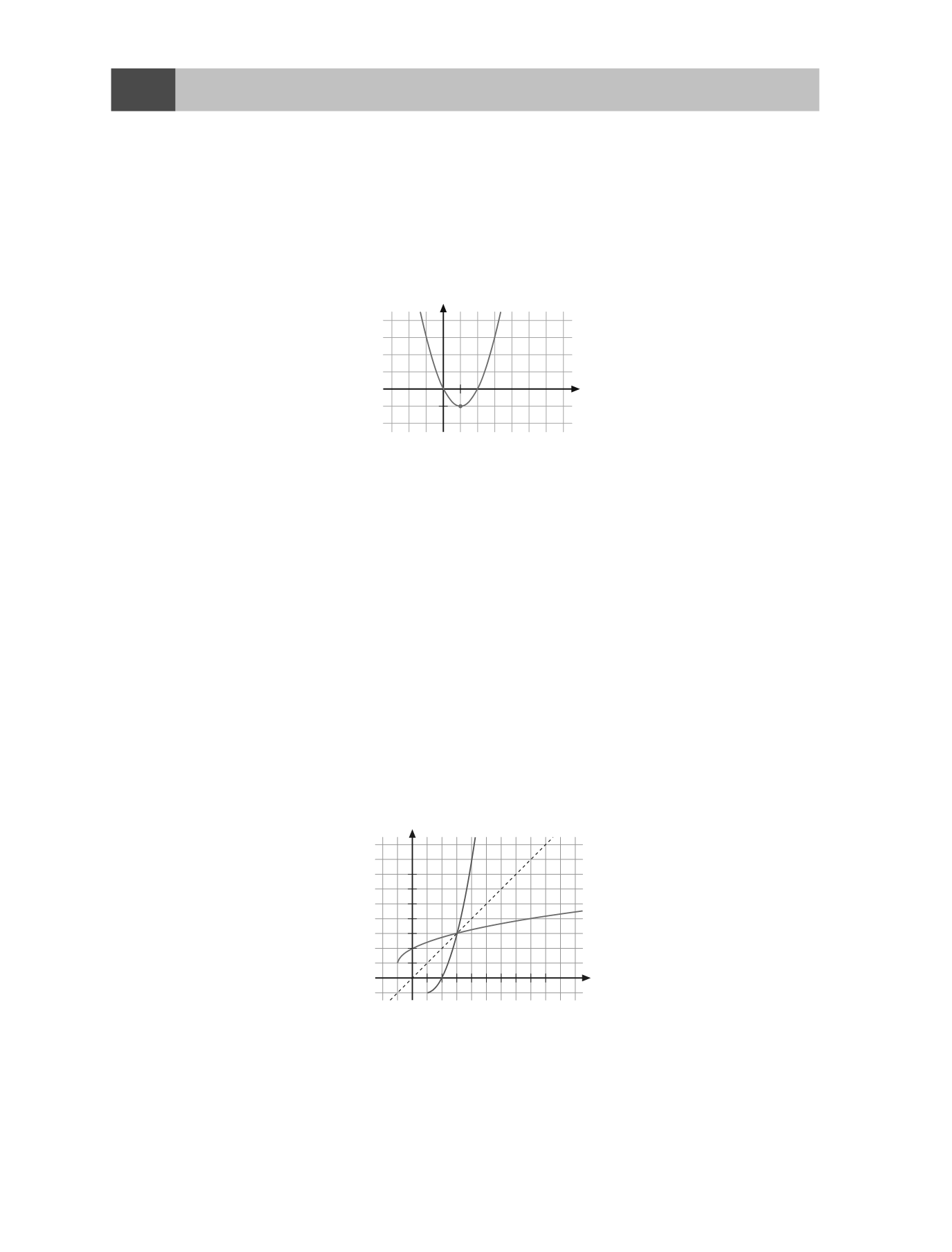
es una función no inyectiva y su representación gráfica es una parábola.
Para conseguir que cada elemento del dominio tenga una sola imagen hay que considerar, o bien el intervalo (
�
∞
, 1],
o el intervalo [1,
�
∞
), porque 1 corresponde al valor de la abscisa del vértice de la parábola.
Si consideramos el dominio como [1,
�
∞
), encontramos otra dificultad:
¿Cómo se aísla la variable
x
de
y
�
x
2
�
2
x
?
Hacemos
x
2
�
2
x
�
y
�
0.
Esta expresión constituye una ecuación de segundo grado que podemos solucionar:
x
�
�
1
�
1
�
y
Permutamos ahora las variables
x
e
y:
y
�
1
�
1
�
x
Esto no es una función, pues, para cada valor de
x
del dominio, se obtienen dos imágenes, por lo tanto, se debe tomar
un solo signo:
y
�
1
�
1
�
x
⇒
f
�
1
(
x
)
�
1
�
1
�
x
El dominio de la función inversa hallada es pues el conjunto de valores reales que cumplen
x
��
1, es decir [
�
1,
�
∞
).
Se observa que este dominio coincide con el recorrido de la función
f
(
x
).
Para su cálculo se debe hallar la ordenada del vértice:
y
�
1
�
2
��
1
Como
a
�
1
�
0, su recorrido es [
�
1,
�
∞
).
2
�
4
�
4
y
��
2
Y
X
1
7
6
5
4
3
2
1
2 3 4 5 6 7 8 9
f
(
x
)
�
x
2
�
2
x
f
�
1
(
x
)
�
1
�
1
�
x
Y
X
1
�
1
V
f
(
x
)
�
x
2
�
2
x


