20
Análisis
Evaluación
(página 235)
)
1.
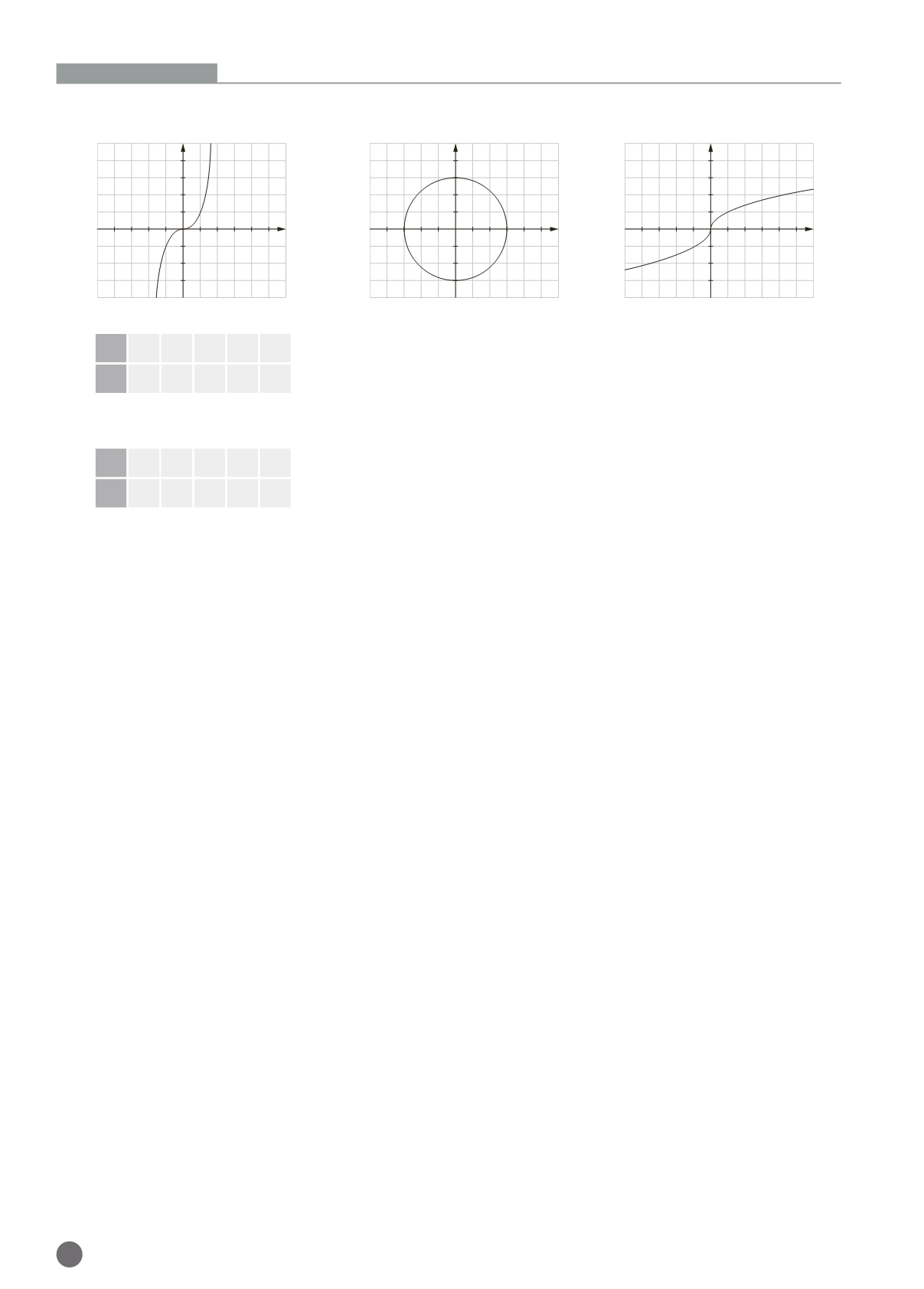
Determina cuáles de las siguientes gráficas corresponden a una función. Construye una tabla de valores y escribe su expresión
analítica.
a)
b)
c)
a)
Corresponde a la función
y
=
x
3
.
b)
No corresponde a una función porque existen valores de la
x
a los que no les corresponde un único valor de la
y
.
c)
Corresponde a la función
y
3
x
.
2.
Halla el dominio de las siguientes funciones.
a)
f
(
x
)
x
1
1
b)
f
(
x
)
x
2
5
x
c)
f
(
x
)
x
2
3
9
d)
f
(
x
)
x
3
3
x
x
4
e)
f
(
x
)
1
x
2
a)
x
1 0
⇒
x
1
⇒
Dom
f
{1}
b)
Es una función polinómica. Dom
f
c)
x
2
9 0
⇒
x
3
⇒
Dom
f
{ 3, 3}
d)
x
0
⇒
Dom
f
{0}
e)
1
x
2
0
⇒
Dom
f
[ 1, 1]
3.
Estudia el signo de estas funciones.
a)
f
(
x
)
x
2
x
1
b)
f
(
x
)
x
2
x
5
x
5
6
c)
f
(
x
)
x
3
3
x
x
4
d)
f
(
x
)
x
2
3
x
2
a)
El signo es constante en los intervalos (
∞
,
1), ( 1, 0), (0, 1) y (1,
∞
).
f
( 2) 0
⇒
f
es negativa en (
∞
,
1).
f
( 0,5) 0
⇒
f
es positiva en ( 1, 0).
f
(0,5)
0
⇒
f
es negativa en (0, 1).
f
(2) 0
⇒
f
es positiva en (1,
∞
).
b)
El signo es constante en los intervalos (
∞
, 2), (2, 3), (3, 5) y (5,
∞
).
f
(0)
0
⇒
f
es negativa en (
∞
, 2).
f
(2,5)
0
⇒
f
es positiva en (2, 3).
f
(4)
0
⇒
f
es negativa en (3, 5).
f
(6)
0
⇒
f
es positiva en (5,
∞
).
c)
El signo es constante en los intervalos (
∞
,
2), ( 2, 1), (1, 2), (2, 4) y (4,
∞
).
f
( 3)
0
⇒
f
es positiva en (
∞
,
2).
f
(0)
0
⇒
f
es negativa en ( 2, 1).
f
(1,5)
0
⇒
f
es positiva en (1, 2).
f
(3)
0
⇒
f
es negativa en (2, 4).
f
(5)
0
⇒
f
es positiva en (4,
∞
).
d)
El signo es constante en los intervalos (
∞
,
2), ( 2,
1), ( 1,
∞
).
f
( 3)
0
⇒
f
es positiva en el intervalo (
∞
,
2).
f
( 1,5)
0
⇒
f
es negativa en el intervalo ( 2,
1).
f
(0)
0
⇒
f
es positiva en el intervalo ( 1,
∞
).
1
O
1
X
Y
O
1
1
X
Y
O
1
1
X
Y
x
f
(
x
)
2
8
1
1
0
0
1
1
2
8
x
f
(
x
)
8
2
1
1
0
0
1
1
8
2


