4.
Estudia la simetría de:
a)
f
(
x
)
x
2
x
2
4
b)
f
(
x
)
x
2
4
x
c)
f
(
x
)
x
3
x
2
5
x
a)
f
(
x
)
(
(
x
)
2
x
)
2
4
x
2
x
2
4
f
(
x
)
Es una función par.
b)
f
(
x
)
(
x
)
2
4 (
x
)
x
2
4
x;
f
(
x
)
x
2
4
x
No es par ni impar.
c)
f
(
x
)
(
x
)
(
3
x
5
)
2
(
x
)
x
3
x
2
5
x
f
(
x
)
Es una función impar.
5.
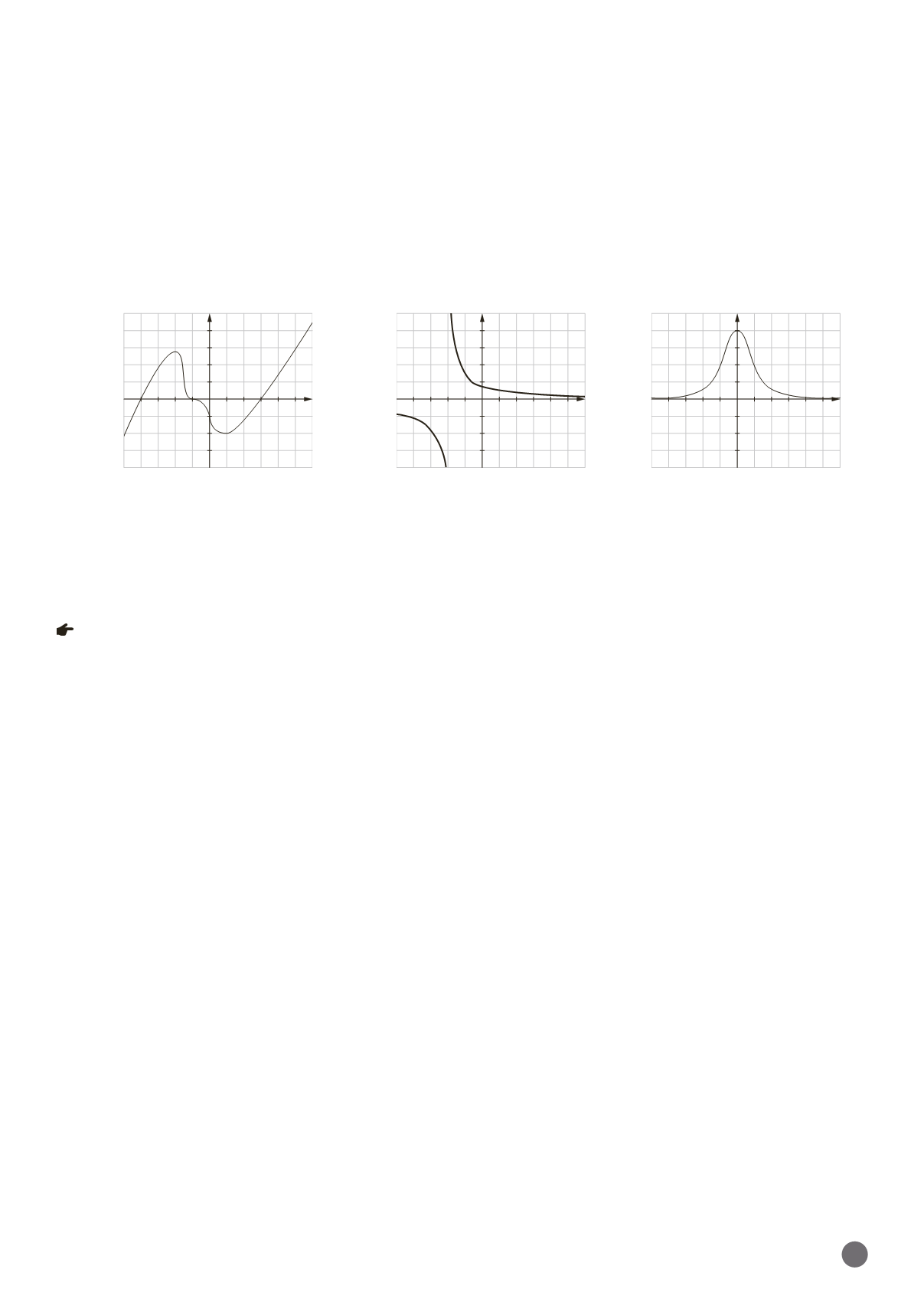
Determina la monotonía y la curvatura de estas funciones. ¿Alguna de ellas está acotada?
a)
b)
c)
a)
Crece en (
∞
,
2)
(1,
∞
) y decrece en ( 2, 1).
Es convexa en el intervalo
∞
,
3
2
( 1, 0) y cóncava en
3
2
,
1
(0,
∞
).
No está acotada.
b)
Es decreciente en todo su dominio. Es convexa en el intervalo (
∞
,
2) y cóncava en ( 2,
∞
). No está acotada.
c)
Crece en el intervalo (
∞
, 0) y decrece en el intervalo (0,
). Es cóncava en el intervalo (
∞
,
1) y en (1,
∞
) y convexa en ( 1, 1).
Está acotada inferiormente por 0 y superiormente por 1.
6.
Determina todas las características de estas funciones.
a)
f
(
x
)
x
2
1
b)
f
(
x
)
x
2
3
x
2
c)
f
(
x
)
x
2
x
d)
f
(
x
)
x
2
4
Todas las funciones son parábolas.
a)
Es positiva en los intervalos (
∞
,
1)
(1,
∞
), y negativa en ( 1, 1).
El vértice es el punto (0,
1), y es el mínimo de la función.
Es decreciente en (
∞
, 0) y creciente en (0,
∞
).
Los puntos de corte con el eje
X
son ( 1, 0) y (1, 0), y el punto de corte con el eje
Y
, (0,
1).
Es una función cóncava.
b)
Es positiva en los intervalos (
∞
, 1) y (2,
∞
), y negativa en (1, 2).
El vértice es el punto
3
2
,
1
4
, y es el mínimo de la función.
Es decreciente en
∞
,
3
2
y creciente en
3
2
,
∞
.
Los puntos de corte con el eje
X
son (1, 0) y (2, 0), y el punto de corte con el eje
Y
, (0, 2).
Es una función cóncava.
c)
Es negativa en los intervalos (
∞
, 0) y (1,
∞
), y positiva en (0, 1).
El vértice es el punto
1
2
,
1
4
, y es el máximo de la función.
Es creciente en
∞
,
1
2
y decreciente en
1
2
,
∞
.
Los puntos de corte con el eje
X
son (0, 0) y (1, 0), y el punto de corte con el eje
Y
, (0, 0).
Es una función convexa.
d)
Es negativa en los intervalos (
∞
,
2) y (2,
∞
), y positiva en ( 2, 2).
El vértice es el punto (0, 4), y es el máximo de la función.
Es creciente en (
∞
, 0) y decreciente en (0,
∞
).
Los puntos de corte con el eje
X
son ( 2, 0) y (2, 0), y el punto de corte con el eje
Y
, (0, 4).
Es una función convexa.
O
1
1
X
Y
O
1
1
X
Y
O
1
1
X
Y
21
8.
Funciones


