4
Ecuaciones
64
AVANZA
Ecuaciones bicuadradas
Las
ecuaciones bicuadradas
son ecuaciones de cuarto grado de la forma
ax
4
+
bx
2
+
c
=
0,
siendo
a,
b
y
c
números conocidos y
a
≠
0.
Para resolverlas, primero se pueden transformar en ecuaciones de segundo grado con un cambio de variable:
p
=
x
2
→
ap
2
+
bp
+
c
=
0
Después, se resuelve la ecuación obtenida, y por último, se deshace el cambio para calcular las posibles soluciones.
Así, para resolver las ecuaciones:
x
4
−
5
x
2
+
4
=
0
x
4
−
3
x
2
−
4
=
0
x
4
+
5
x
2
+
4
=
0
1
Cambiamos la variable:
p
2
−
5
p
+
4
=
0
p
2
−
3
p
−
4
=
0
p
2
+
5
p
+
4
=
0
2
Resolvemos la ecuación de segundo grado que obtenemos:
p
=
5
±
25 16
2
p
1
=
4
p
2
=
1
p
=
3
±
9
+
16
2
p
1
=
4
p
2
=
1
p
=
5
±
25 16
2
p
1
=
1
p
2
=
4
3
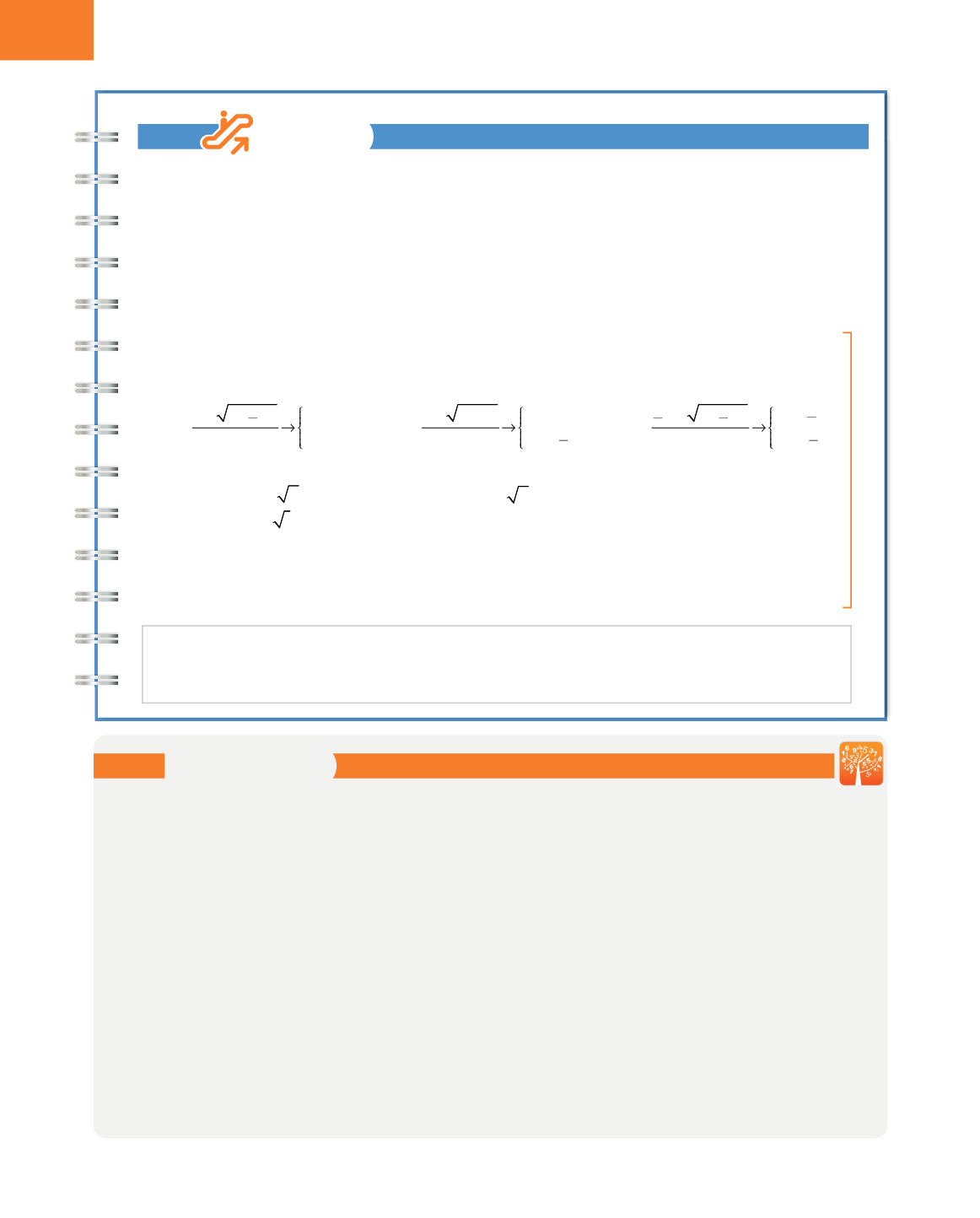
Deshacemos el cambio de variable con cada solución:
x
2
=
4
→
x
= ±
4
= ±
2
x
2
=
1
→
x
= ±
1
= ±
1
⎧
⎨
⎪⎪
⎩
⎪⎪
x
2
=
4
→
x
= ±
4
= ±
2
x
2
=
−
1
→
No tiene solución.
⎧
⎨
⎪⎪
⎩⎪⎪
x
2
=
−
1
x
2
=
−
4
⎧
⎨
⎪⎪
⎩⎪⎪
Las soluciones de
x
4
−
5
x
2
+
4
=
0 son 2,
−
2, 1,
−
1.
Las soluciones de
x
4
−
3
x
2
−
4
=
0 son 2 y
−
2.
La ecuación
x
4
+
5
x
2
+
4
=
0 no tiene solución.
A1.
Calcula las soluciones de las siguientes ecuaciones bicuadradas.
a)
x
4
−
2
x
2
+
1
=
0
c)
x
4
+
5
x
2
−
6
=
0
b)
x
4
+
2
x
2
+
1
=
0
d)
x
4
−
125
x
2
+
484
=
0
CÁLCULO MENTAL
Estrategia para AVERIGUAR UN NÚMERO
❚
Piensa un número positivo.
❚
Súmale 2.
❚
Eleva el resultado al cuadrado.
❚
Réstale ahora el cuádruplo del número siguiente al que pensaste al principio.
❚
Si me dices qué número has obtenido, yo averiguo el número que has pensado.
¿Cómo podemos saber qué número se había pensado?
Si este número es
x,
entonces:
Le sumamos 2:
x
+
2
Elevamos el resultado al cuadrado y obtenemos:
x
+
2
(
)
2
=
x
2
+
4
x
+
4
Restamos el cuádruplo del número siguiente:
x
2
+
4
x
+
4
−
4
x
+
1
(
)
=
x
2
Si calculamos la raíz cuadrada del número obtenido, el resultado es el número pensado.
CM1.
Halla el número positivo que ha pensado Ana si, tras elevar al cuadrado el resultado de sumarle 3 y restar a la
cantidad resultante el séxtuplo del número de partida, obtuvo el número 58.
CM2.
Inventa un procedimiento similar a los anteriores para averiguar el número que ha pensado otra persona.


