11
Perímetros y áreas de polígonos
226
``
Calcula el área de un triángulo isósceles cuyos lados miden 34 cm, 34 cm y 32 cm, respectivamente.
Solución
La altura divide al triángulo en dos triángulos
Aplicamos el teorema de Pitágoras en uno de los
rectángulos.
triángulos rectángulos.
34 cm
34 cm
32 cm
h
34 cm
16 cm
h
h
2
+
16
2
=
34
2
h
2
+
256
=
1156
h
2
=
1156
−
256
h
2
=
900
h
=
30 cm
La altura del triángulo isósceles mide 30 cm y su área es de
:
A
32 30
2
480 cm
2
⋅
=
=
EJERCICIO RESUELTO
6.
ÁREA DE TRIÁNGULOS
Eva y sus amigos están preparando
banderines para adornar las calles
durante las fiestas de su pueblo.
Eva ha observado que, a pesar de
que todos los banderines tienen
forma triangular y poseen la
misma altura y la misma base, son,
sin embargo, triángulos diferentes.
Se pregunta entonces cuál tendrá
mayor superficie. Para averiguarlo,
los coloca sobre una cuadrícula de
1 cm de lado.
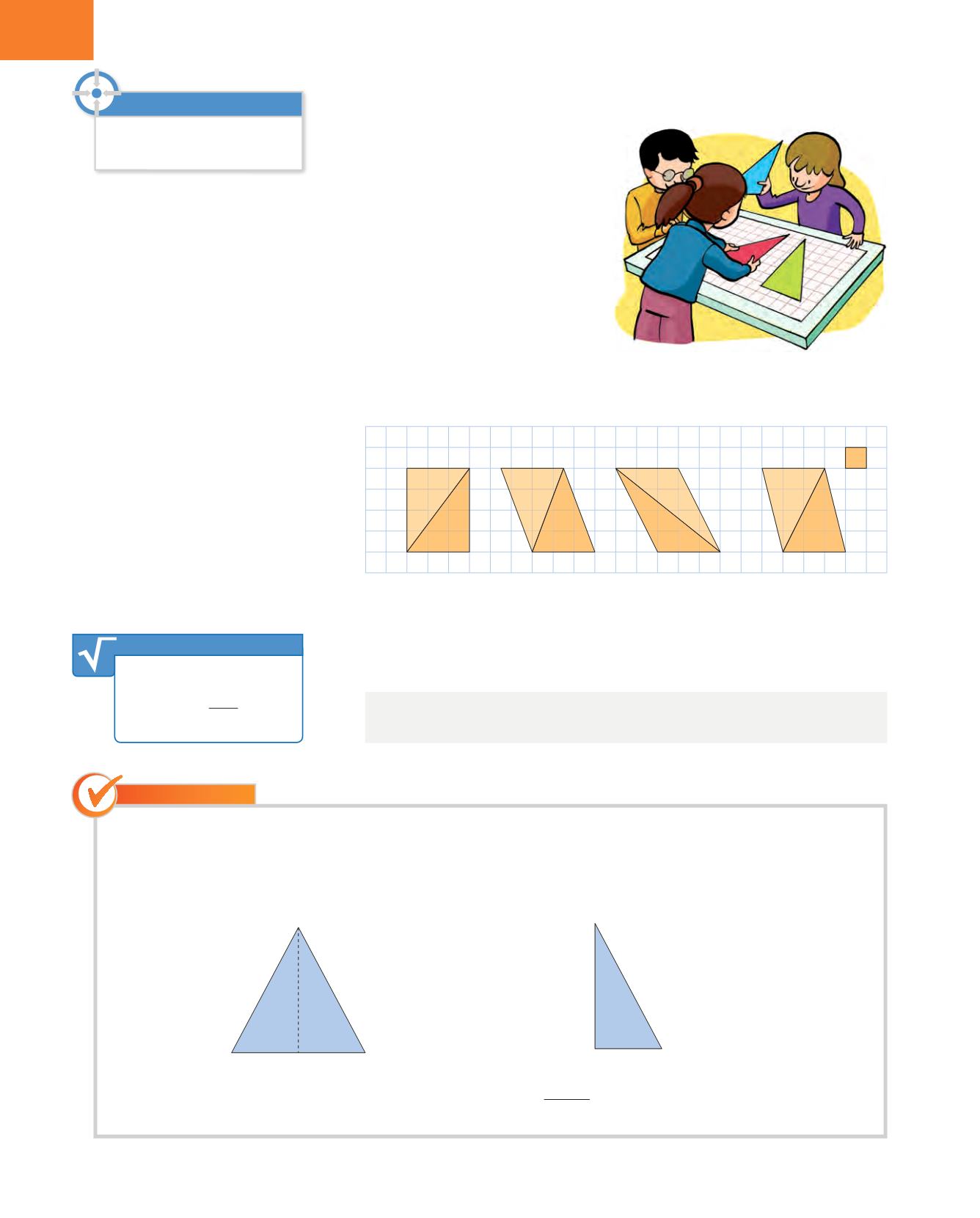
Para calcular el área de cada uno, pone otro banderín de las mismas dimensiones
para formar cuadrados o romboides, cuya área ya sabe calcular.
1cm
2
El área de todos los cuadriláteros es la misma
:
4
⋅
3
=
12 cm
2
Como cada cuadrilátero contiene dos triángulos iguales, el área de un triángulo
es la mitad que la de los cuadriláteros.
El
área de un triángulo
es el resultado de multiplicar su base por su altura
y dividirlo por dos
.
Aprenderás a…
❚●
Calcular el área de un
triángulo.
Área del triángulo:
⋅
A
b h
2
=
Lenguaje matemático


