11
Perímetros y áreas de polígonos
228
7.
ÁREA DE POLÍGONOS REGULARES
En el parque de un pueblo van a instalar un templete para que la banda de
música pueda dar conciertos.
Los técnicos del Ayuntamiento han elaborado varios proyectos distintos basados
en polígonos regulares cuyos lados miden 3 m. Solo disponen de un espacio de
40 m
2
y quieren elegir el templete que tenga mayor superficie.
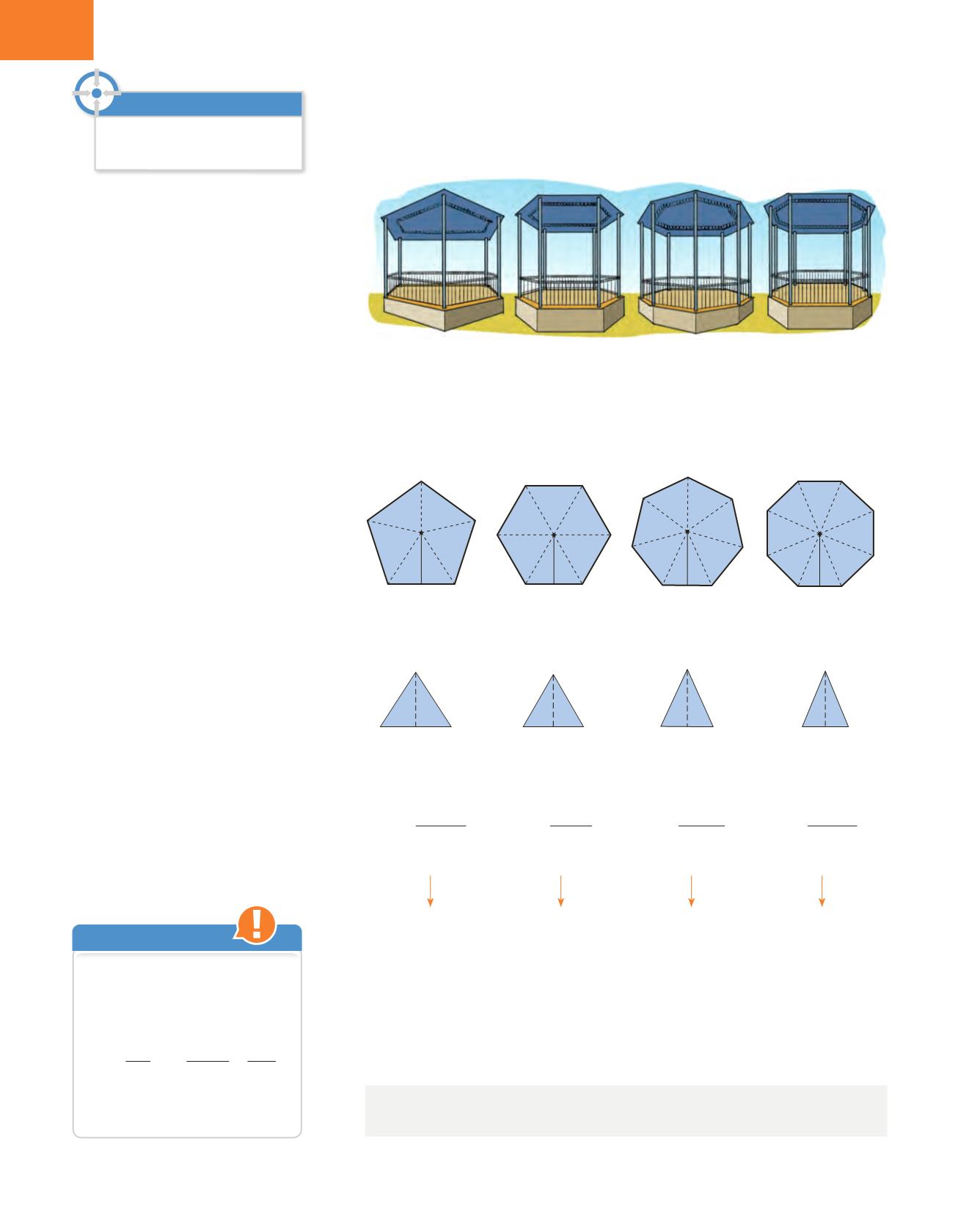
Para decidir qué base tendrá el templete, podemos descomponer cada polígono
regular en tantos triángulos iguales como lados tenga.
3 m
3 m
3 m
3 m
2,06 m
2,6 m
3,11 m
3,62 m
La base de cada triángulo coincide con el lado del polígono, y la altura, con su
apotema.
3 m
3 m
3 m
3 m
2,06 m
2,6 m
3,11 m
3,62 m
Calculamos el área de uno de estos triángulos y la multiplicamos por el número
de lados del polígono.
=
=
=
A
A
3 2,06
2
3,09 m
T
T
2
⋅
=
=
=
A
A
3 2,6
2
3,9 m
T
T
2
⋅
=
=
=
A
A
3 3,11
2
4,665 m
T
T
2
⋅
=
=
=
A
A
3 3,62
2
5,43 m
T
T
2
⋅
Área del
pentágono
Área del
hexágono
Área del
heptágono
Área del
octógono
A
=
5
⋅
3,09
=
A
=
15,45 m
2
A
=
6
⋅
3,9
=
A
=
23,4 m
2
A
=
7
⋅
4,665
=
A
=
32,655 m
2
A
=
8
⋅
5,43
=
A
=
43,44 m
2
Al comparar las áreas obtenidas, deciden instalarlo en forma de heptágono,
ya que no disponen de superficie suficiente para levantarlo en forma de
octógono.
El
área de un polígono regular
es igual a su lado por su apotema dividido
por dos y multiplicado por su número de lados
.
Aprenderás a…
❚●
Calcular el área de un
polígono regular.
Presta atención
Como en un polígono regular el
perímetro es igual al número de
lados por la longitud del lado, la
fórmula de su área también es:
⋅
⋅
⋅ ⋅
⋅
A
l a
n
l n a P a
2
2
2
=
=
=
donde
P
es el perímetro, y
a,
la
apotema.


