224
11
Funciones
6.
INTERPRETACIÓN DE GRÁFICAS
Un grupo de amigos está pasando el fin de semana en un
camping
que tiene un
depósito de agua para las duchas.
Se levantaron a las 6 h de la mañana y no pudieron ducharse porque el depósito
estaba vacío. Decidieron salir a correr y luego preparar el desayuno hasta que el
depósito de agua se hubiera llenado.
Entre las 7 h y las 8 h no utilizaron las duchas, pero de 8 h a 9 h gastaron 4 m
3
.
Emplearon la siguiente hora en ir al supermercado a comprar.
De 10 h a 11 h utilizaron para la limpieza el agua que quedaba en el depósito.
Esta gráfica, que relaciona el
tiempo
y el
volumen
, representa el estado del depósito
de agua desde las 6 h hasta las 11 h de la mañana.
Para interpretarla, vamos a estudiar todas las características de la función.
Aprenderás a…
●
Describir con el lenguaje
apropiado, a partir de una
gráfica, las características de
una función.
●
Analizar gráficas que
representan fenómenos del
entorno cotidiano y formular
conjeturas.
EJERCICIO RESUELTO
``
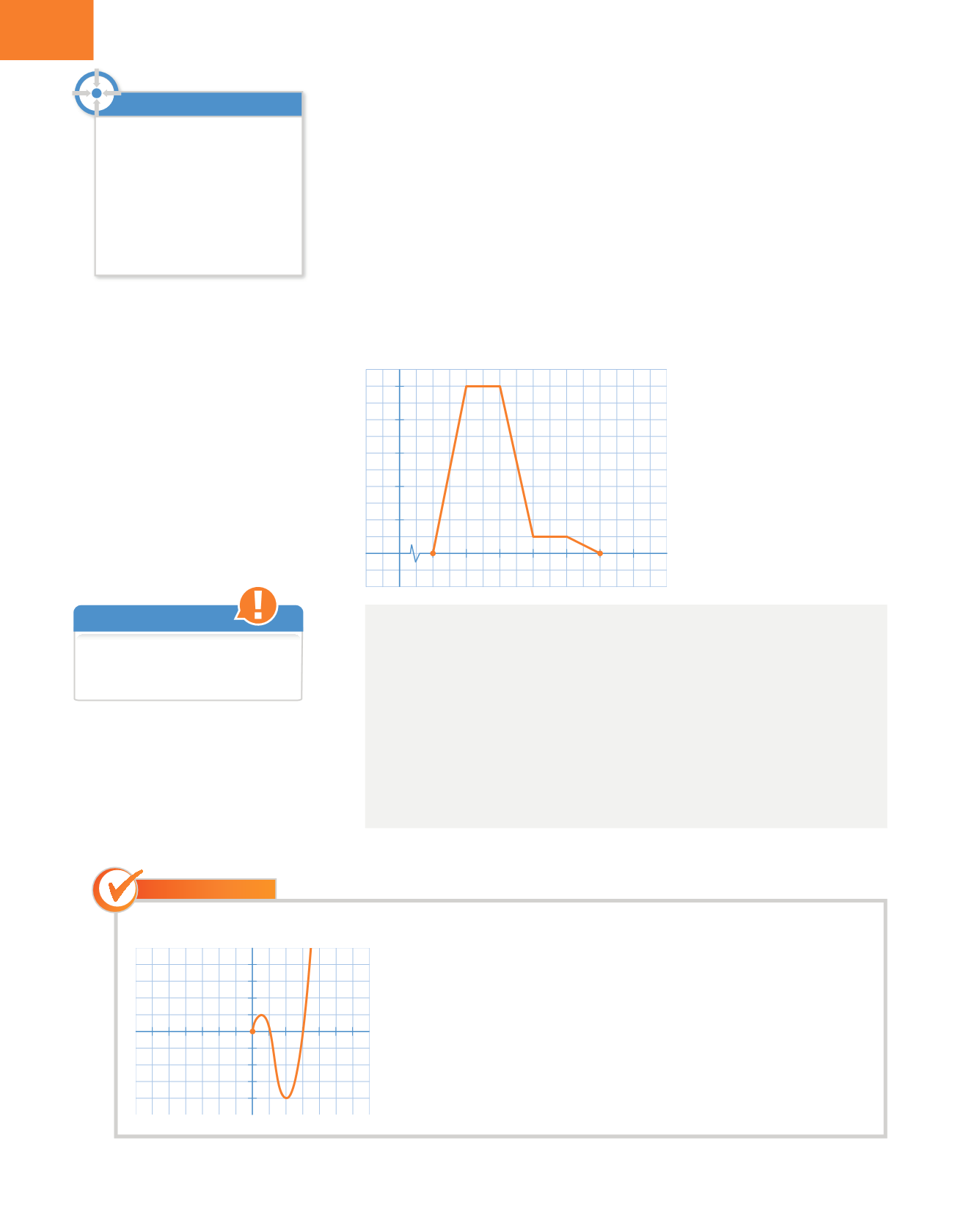
Observa la gráfica y describe todas las características de la función.
Solución
Dominio: [0,
+
∞
)
Recorrido: [
−
4,
+
∞
)
Puntos de corte:
❚
Con el eje
X:
(0, 0), (1, 0) y (3, 0)
❚
Con el eje
Y:
(0, 0)
Continuidad: Es continua.
Es creciente en (0; 0,5) y en (2,
+
∞
).
Es decreciente en (0,5; 2).
Máximo: (0,5; 1)
Mínimo: (2,
−
4)
Simetrías: No es par ni impar.
Periodicidad: No es periódica.
O
1
1
X
Y
Dominio: [6, 11]
Recorrido: [0, 5]
Puntos de corte:
❚
Con el eje
X
: (6, 0) y (11, 0)
❚
No tiene con el eje
Y
.
Es creciente en (6, 7).
Es decreciente en (8, 9) y (10, 11).
Es constante en (7, 8) y (9, 10).
No tiene máximos ni mínimos.
Al
interpretar la gráfica de una función
hay que seguir estos pasos:
❚
Reconocer la variable independiente y la dependiente.
❚
Identificar el dominio y el recorrido de la función.
❚
Hallar los puntos de corte con los ejes.
❚
Decidir si la función es continua.
❚
Analizar los intervalos de crecimiento y decrecimiento.
❚
Establecer si la función tiene máximos y mínimos.
❚
Determinar si se trata de una función simétrica.
❚
Distinguir si es una función periódica.
O
6
1
X
Y
7 8 9 10 11
2
3
4
5
Presta atención
Cuando interpretamos la gráfica de
una función, estudiamos la gráfica de
izquierda a derecha.


