234
El precio de un viaje en tren es función, entre otras
cosas, de los kilómetros recorridos. Recorrer 57 km cuesta
2,21
€
y recorrer 68 km vale 2,54
€
. Averigua:
a)
La función afín que expresa el coste del billete en fun-
ción de los kilómetros recorridos.
b)
Por extrapolación, el precio del billete cuando la dis-
tancia recorrida sea de 500 km.
c)
Si un billete cuesta 5,93
€
, ¿cuántos kilómetros tiene el
recorrido?
Solución:
b)
15,50
€
c)
181 km
Encuentra una función cuadrática
f
(
x
) que tome los
valores que muestra la tabla:
Expresa el volumen de un cono cualquiera de gene-
ratriz 2 dm en función de su altura. ¿Entre qué valores pue-
de oscilar la altura? Indica el dominio de esta función.
Solución:
La altura oscila entre 0 y 2 dm.
Si un juguete se vende a 130
€
lo compran 1 000
personas. Por cada euro que aumenta (o disminuye) este
precio, disminuye (o aumenta), respectivamente, el número
de compradores en 50.
a)
Expresa la función que proporciona el número de ju-
guetes que se venden en función del precio de venta.
b)
Si el precio de coste de un juguete es de 80
€
, calcula
el precio,
p,
que proporciona el beneficio total máximo.
c)
Halla el número de juguetes que se venden si el precio
es
p,
y calcula el beneficio máximo.
Solución:
b)
115
€
c)
1 750 juguetes y 61 250
€
de beneficio
El perímetro de un triángulo isósceles es 6 cm. Ex-
presa el área del triángulo en función de la base,
b,
y deter-
mina su dominio.
Expresa el área de un pentágono regular en función
de su lado,
l,
y determina su dominio.
El área de un contenedor forma-
do por una semiesfera de radio
r
y un
cilindro abierto de altura
h
es de 32 m
2
.
Expresa su volumen en función del ra-
dio, y determina su dominio.
En un cubo se instala un de-
pósito en forma de pirámide inver-
tida con la misma base que la cara
superior del cubo.
Determina el área de la cuatro ca-
ras del depósito, en función de su
volumen.
Un almacén tiene forma de prisma recto de base
cuadrada y su volumen es 768 m
3
. Se sabe que la pérdida
de calor a través de las paredes laterales es de 100 unida-
des por m
2
, mientras que por el techo es de 300 unidades
por m
2
. La pérdida de calor a través del suelo es desprecia-
ble. Expresa la pérdida de calor del almacén en función del
lado de su base.
61
60
59
58
57
56
55
54
53
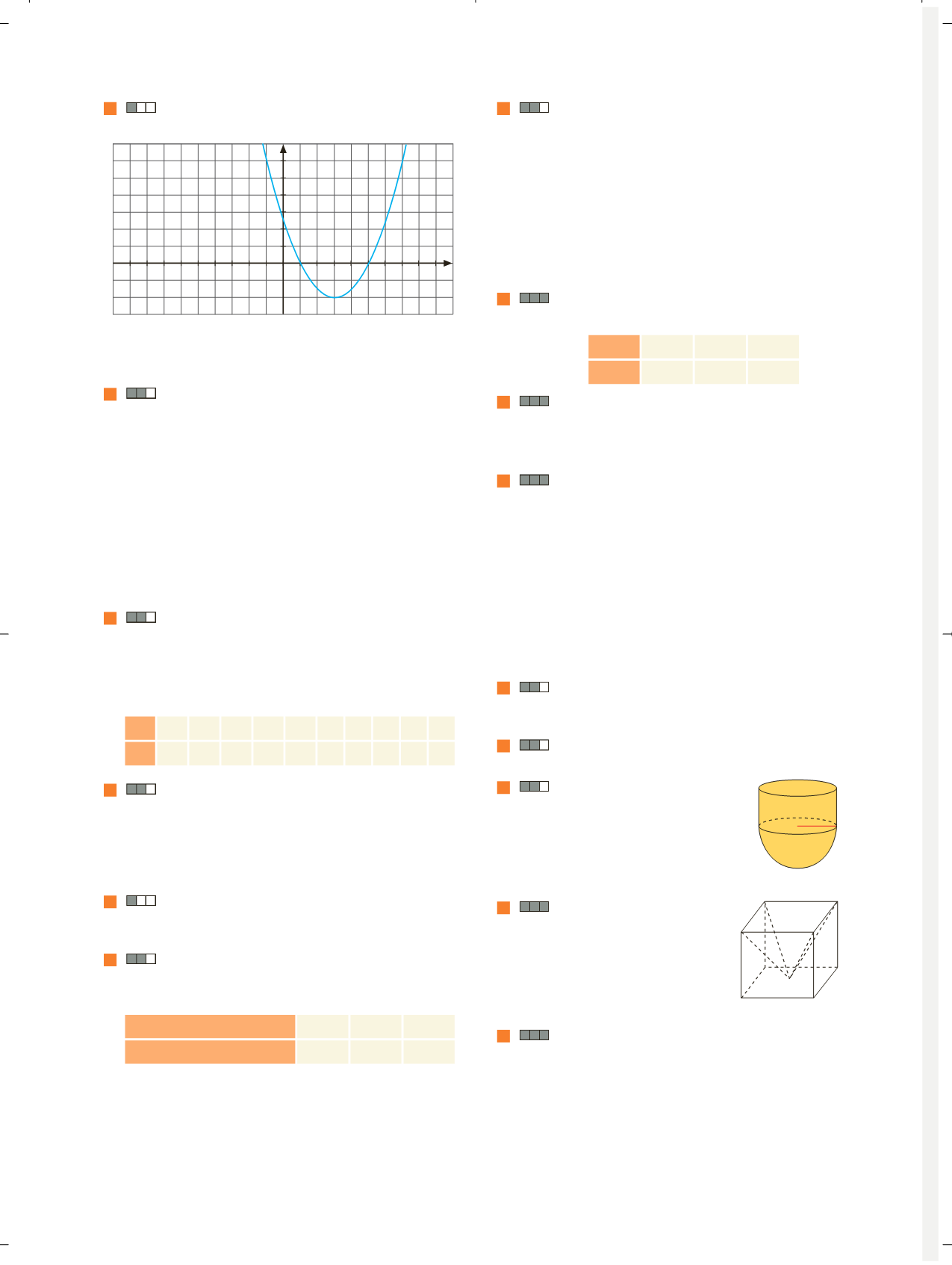
A partir de la gráfica de la función
f
(
x
) de la figura,
representa:
f
(
x
),
f
(
x
),
f
(
x
3),
f
(
x
) 3 y 2
f
(
x
).
F
IGURA
8.58.
Ejercicios de aplicación
Considera las siguientes funciones:
f
(
x
) 2
x
2
3
x
1
g
(
x
)
(
x
1)
2
h
(
x
)
x
2
x
1
i
(x)
3
x
2
x
2
a)
Represéntalas gráficamente, indicando sus ceros, sus
vértices y sus ejes de simetría.
b)
Estudia su signo.
c)
Indica sus intervalos de monotonía y sus recorridos.
d)
Escribe las funciones valor absoluto correspondientes
a cada una como funciones a trozos, y represéntalas.
Dada la función
f
(
x
)
x
3
3
x
2
9
x:
a)
Averigua sus ceros.
b)
Determina sus intervalos de signo constante.
c)
Esboza una gráfica, completando previamente la si-
guiente tabla de valores:
La tarifa del transporte en ta
x
i en cierta localidad
depende linealmente de la longitud del trayecto que se
efectúe. A un usuario de este servicio, una carrera de 3,6
km le cuesta 7,12
€
, y a otro, 8,80
€
un trayecto de 5 km.
¿Cuánto vale la bajada de bandera?
Solución:
2,80
€
Una función lineal pasa por los puntos ( 1, 5/2) y
(1/4,
3). Halla su expresión analítica. ¿Es una función cre-
ciente?
El porcentaje destinado de I D del PIB de un deter-
minado país en los años 2008, 2010 y 2012 es la que se in-
dica en la siguiente tabla:
Mediante interpolación lineal, calcula el porcentaje del PIB
destinado de I D en el año 2009 y realiza una extrapola-
ción para estimar cuánto se destinará en el año 2016.
Solución:
En 2009, fue de un 0,33%.En 2016 será del 0,68%.
52
51
50
49
48
47
x
f
(
x
)
5
4
3
2
1 1 2 3 4 5
Año
% I D del PIB
2008
0,28
2010
0,32
2012
0,47
x
f
(
x
)
0
1,25
2
0,75
1
6,75
O
X
Y
5
5
5
h
r
F
IGURA
8.59.
a
F
IGURA
8.60.


