229
La gráfica muestra la relación entre la altura sobre el nivel del mar y la temperatura. Como
se puede observar, la relación es lineal, y resulta posible averiguar su expresión analítica. La
función que proporciona la temperatura en relación con la altura se designa
T
(
h
) y debe ser
del tipo
T
(
h
)
m h n,
es decir, se trata de una función polinómica de primer grado.
Dado que hemos de determinar dos coeficientes, necesitamos dos puntos. Observando la
gráfica, escogemos (0, 15) y (10 000,
50).
Sustituimos estos valores en la expresión de
T
(
h
):
15
m
0
n
50
m
10 000
n
Por tanto,
n
15 y
m
0,0065.
La función es:
T
(
h
)
0,0065
h
15
Se obtiene la misma expresión utilizando la ecuación punto pendiente de la recta, deter-
minando previamente la pendiente:
m
( 50
15)/(10 000
0)
0,0065
Entonces, escogemos un punto:
T
(
h
)
15
( 0,0065)(
h
0)
⇒
T
(
h
)
15
0,0065
h
7.
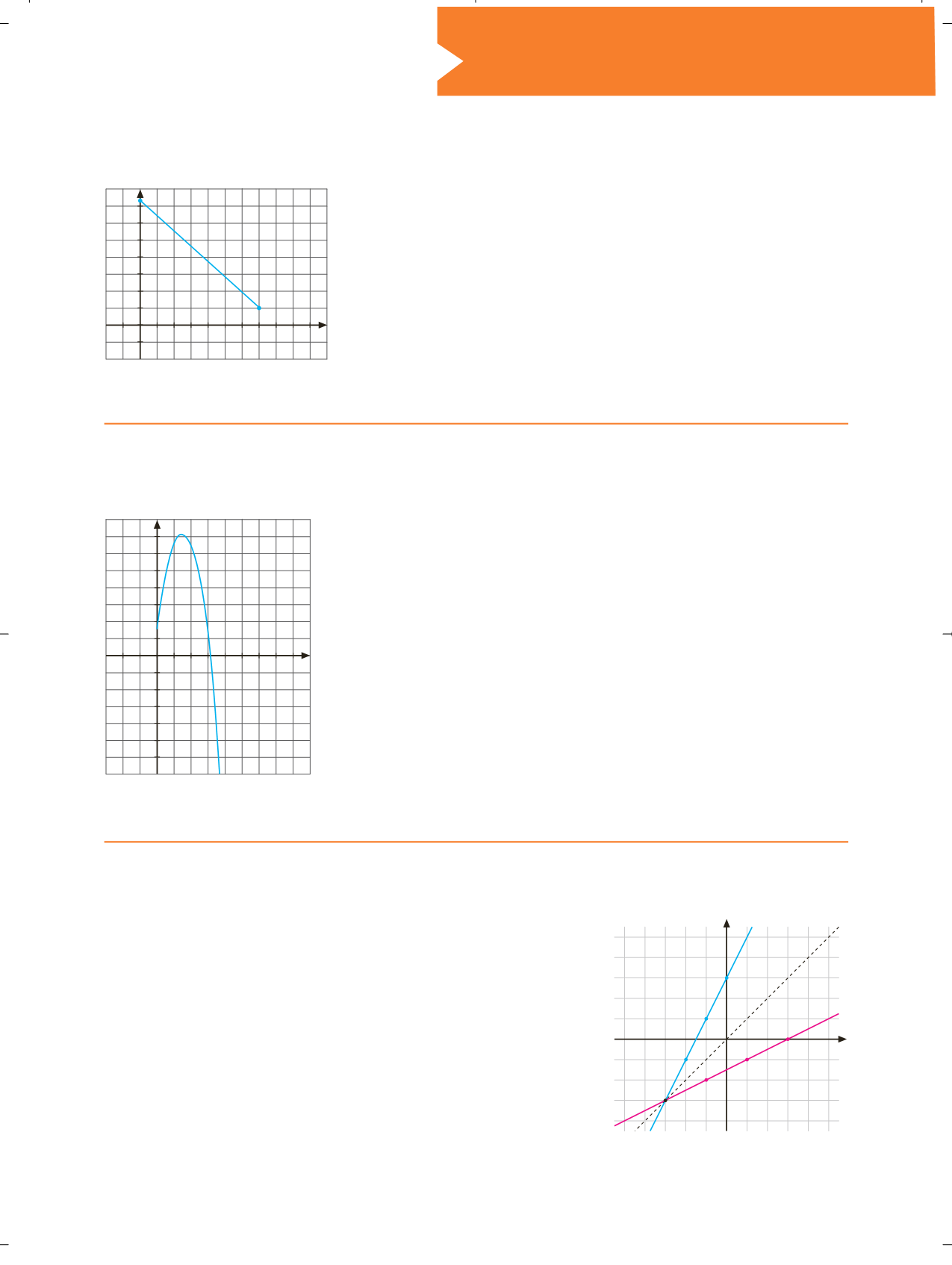
Averiguar la expresión analítica
que corresponde a la gráfica:
O
1 000
temperatura(ºC)
altura sobre el nivel del mar (m)
5 000 10 000 15 000
50
40
30
20
10
0
10
F
IGURA
8.46.
Dado un sistema de referencia, la gráfica que relaciona el tiempo con la posición en un
movimiento uniformemente acelerado es de una función polinómica de segundo grado:
s
(
t
)
s
0
v
0
t a t
2
/2
s
0
,
v
0
y
a
son los coeficientes de esta función.
s
0
es la posición inicial, o el punto que corresponde al momento
t
= 0
v
0
es la velocidad inicial
a
es la aceleración del movimiento
A partir de la gráfica se conocen tres puntos: (0, 3), (1, 13) y (3, 3). Con estos puntos se puede
obtener la expresión de la posición del móvil en cada instante haciendo:
s
(0)
3
⇒
3
s
0
v
0
0
a
0
2
/2
s
(1)
13
⇒
13
s
0
v
0
1
a
1
2
/2
s
(3)
3
⇒
3
s
0
v
0
3
a
3
2
/2
Es preciso, pues, resolver un sistema de tres ecuaciones con tres incógnitas. De la primera
ecuación se obtiene directamente:
s
0
3.
Sustituyendo en la tercera ecuación se tiene que:
v
0
3
a
/2
De la segunda ecuación se obtiene: 13
3
3
a
/2
a
/2
⇒
a
10, con lo que
v
0
15
La ecuación posición-tiempo buscada es:
s
(
t
)
3
15
t
5
t
2
Interpolación cuadrática
8.
Determinar la ecuación
posición-tiempo correspondiente
a la siguiente gráfica.
F
IGURA
8.47.
2
4
6
8
O
t
(
s
)
1 2 3 4 5
2
4
s
(
m
)
10
12
14
6
8
10
6 7
2
Dos funciones que son inversas respecto de la composición tienen intercambiados el do-
minio y el recorrido; es decir, los pares de valores, (
x, f
(
x
)), que corresponden a los puntos de
la gráfica de
f
(
x
), están intercambiados en
la gráfica de
f
1
(
x
) y son: (
f
(
x
),
f
1
(
f
(
x
)), es
decir, (
f
(
x
),
x
).
Gráficamente, esto se traduce en una si-
metría respecto de la recta
y x.
Se consideran algunos puntos de la recta
f
(
x
): (0, 3), ( 1, 1), ( 2,
1), ( 3,
3)
Y para representar
f
1
(
x
) se intercambian
las coordenadas así tenemos: (0, 3), (1,
1),
( 1,
2), ( 3,
3).
Gráficas de funciones inversas respecto de la composición
9.
Representa las gráficas
de
f
(
x
)
2
x
3 y
f
1
(
x
).
F
IGURA
8.48.
X
Y
f
(
x
)
f
1
(
x
)
EJERCICIOS RESUELTOS


