233
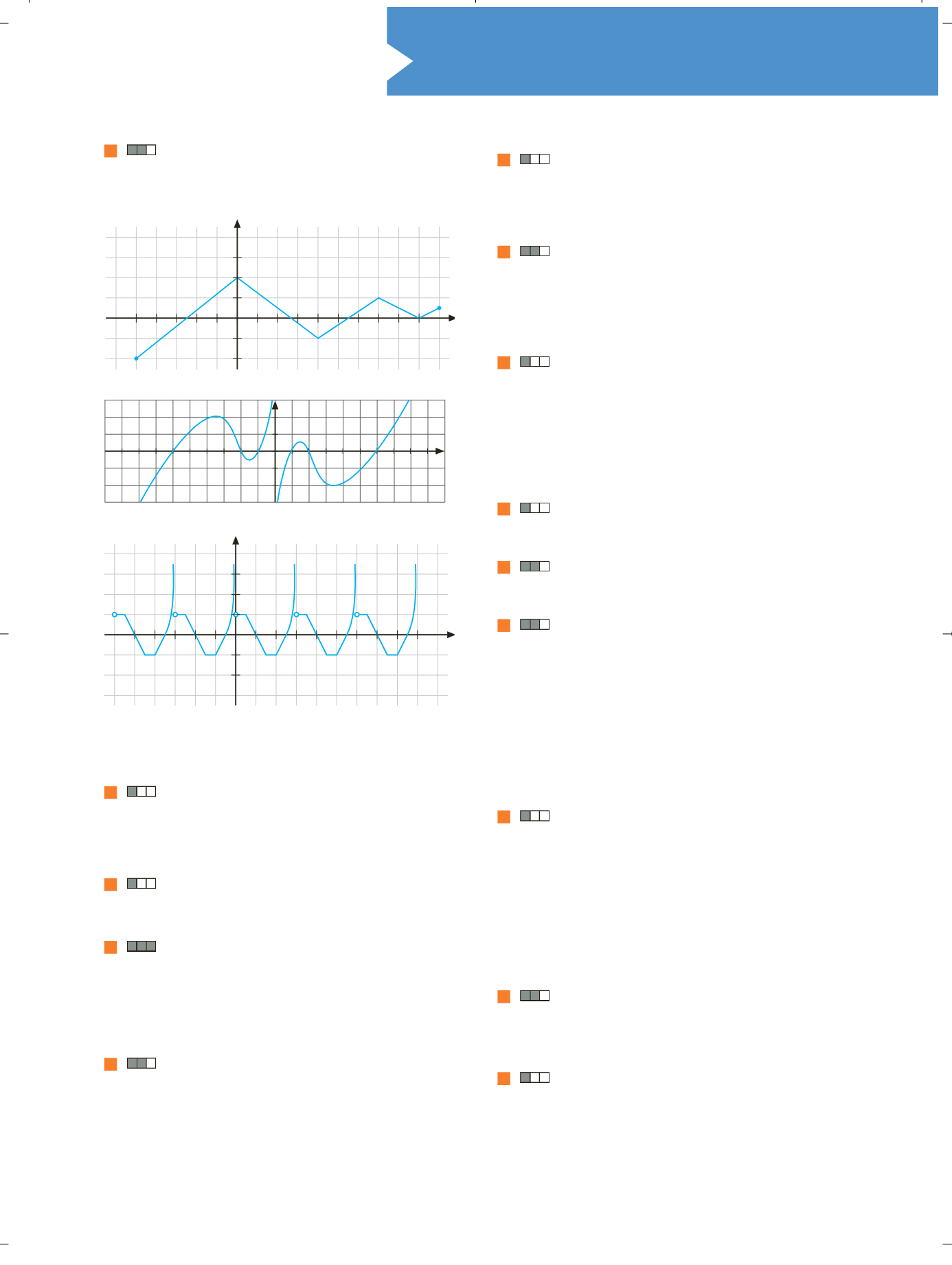
Estudia en las funciones que muestran las figuras,
los intervalos de signo constante, la monotonía y la curva-
tura si es posible. ¿Está acotada alguna de las funciones?
¿Hay alguna que presente simetría? ¿Y periodicidad?
Operaciones con funciones
Calcula, en cada caso, (
f g
)(
x
) y su dominio:
a)
f
(
x
)
x
3
2
x
2
x
3,
g
(
x
)
x
2
4
b)
f
(
x
)
2
x
3
x
1
,
g
(
x
)
x
1
2
Calcula (
f g
)(
x
) y (
f g
)(
x
), y sus respectivos domi-
nios, siendo
f
(
x
)
1
x
y
g
(
x
)
1
x
2
x
.
Dadas las siguientes funciones definidas a trozos,
calcula (
f g
)(
x
) y su dominio:
f
(
x
)
x
2
2
1
si
x
3
x
2
1 si
x
3
Calcula, en cada caso, (
f
·
g
)(
x
) y su dominio:
a)
f
(
x
)
x
2
x
1
,
g
(
x
)
x
x
2
1
x
b)
f
(
x
)
x
2
x
6,
g
(
x
)
2
x
x
2
6
37
36
35
34
33
Halla (
f g
)(
x
), (
f g
)(
x
),
g
f
(
x
), y sus respectivos
dominios, a partir de las funciones:
f
(
x
)
x
3
2
3
x
x
y
g
(
x
)
x
2
3
x
4
x
5
3
Dadas las funciones definidas a trozos:
f
(
x
)
x
2
si
x
0
y
x
si
x
0
encuentra la expresión de (
f · g
)(
x
) y su dominio.
A partir de los siguientes pares de funciones, halla
(
f g
)(
x
) y (
g f
)(
x
), indicando su dominio:
a)
f
(
x
)
3
2
x
,
g
(
x
)
2
3
x
b)
f
(
x
)
x
2
1,
g
(
x
) 3
c)
f
(
x
) 2
x
2
x
3
, g
(
x
)
x
1
1
Dadas las funciones
f
(
x
)
y
g
(
x
)
2
x
1,
calcula la función compuesta de
f
(
x
) y
g
(
x
) y su dominio.
A partir de las funciones
f
(
x
) 2
x x
2
y
g
(
x
)
x
2,
halla (
f g
)(
x
) y (
g f
)(
x
) y sus respectivos dominios. ¿Qué se
observa? ¿Es siempre posible la composición?
La función
h
(
x
) 4
x
2
se puede entender como la
composición de las funciones
f
(
x
) 2
x
y
g
(
x
)
x
2
de este
modo: (
g f
)(
x
)
g
(
f
(
x
))
g
(2
x
) 4
x
2
h
(
x
).
Expresa las siguientes funciones como composición de
funciones, indicando estas últimas:
a)
h
(
x
) 5
x
5
b)
h
(
x
) 5
x
4
2
x
2
6
Función inversa
¿Existe función inversa respecto de la composición
para las siguientes funciones? Si es así, halla su expresión.
a)
f
(
x
) 3
x
2
e)
f
(
x
)
4
x
1
2
b)
f
(
x
)
x
4
x
3
f)
f
(
x
)
x
1
x
c)
f
(
x
)
3
x
8
g)
f
(
x
)
x
2
3
x
1
d)
f
(
x
)
x
2
5
x
h)
f
(
x
)
1
4
x
Representa la función
f
(
x
)
x
1 y su inversa.
Transformaciones de funciones
A partir de la función
f
(
x
)
1
x
, representa las siguien-
tes funciones e indica sus dominios y recorridos:
a)
f
(
x
)
x
1
2
b)
f
(
x
) 2
x
1
2
c)
f
(
x
)
3
1
x
46
45
44
43
42
2
x
x
1
41
40
39
38
g
(
x
)
x
1
1
si
x
0
x
1
1
si
x
0
Y
X
O
3
2
1
2
1 2 3 4 5 6 7
1 2 3 4 5
8 9
Y
X
O
3
1
2
1
2
2 3 4 5 6 7 8 9
1 2 3 4 5
1
2
O
X
1 2 3 4
Y
5 6 7 8 9
2
2 4 6 8
F
IGURA
8.57.c.
F
IGURA
8.57.b.
F
IGURA
8.57.a.
g
(
x
)
1
x
si
x
0
x
3
si
x
0
EJERCICIOS Y PROBLEMAS


