253
Movimientos en una y dos dimensiones
ACTIVIDADES Y TAREAS
10
48
Una rueda de 0,5 m de radio gira con un período
de 0,6 s. Determina la aceleración centrípeta de los
puntos de su periferia.
Solución:
54,8 m/s
2
49
Un ciclista marcha con su bicicleta de montaña, cu-
yas ruedas tienen un diámetro de 26 pulgadas, a
una velocidad constante de 25 km/h.
a)
¿Cuántas vueltas habrán dado sus ruedas en 15 min?
b)
¿Cuál es el radio de dichas ruedas?
c)
¿Qué velocidad angular llevan?
d)
¿Cuál es su período y su frecuencia mientras giran de
esa manera?
Dato: 1 pulgada = 2,54 cm
Solución:
a)
3012,5 vueltas;
b)
33 cm;
c)
21,03 rad/s;
d)
0,29 s; 3,34 s
−
1
50
Por la periferia de una pista circular parten a la vez,
del mismo punto y en direcciones opuestas, dos mó-
viles con velocidades de 4 rpm y 1,5 rpm, respectiva-
mente. ¿En qué punto se encontrarán y qué tiempo
habrá transcurrido?
Solución:
Cuando el primero describa 4,57 rad; 10,9 s
51
Un cuerpo que describe círculos de 10 cm de radio
está sometido a una aceleración centrípeta cuyo
módulo constante en cm/s
2
es, numéricamente, el
doble del módulo de su velocidad lineal expresada
en cm/s. Determina los módulos, direcciones y senti-
dos de los vectores
a
c
,
v
y
ω
y el número de vueltas
que dará el móvil en 1 min.
Solución:
a
c
=
40 cm/s
2
, radial hacia el centro;
v
=
20 cm /s
2
, tangencial;
ω
=
2 rad/s, perpendicular al plano;
19 vueltas
52
Una máquina de equilibrado de ruedas de coche
hace que estas giren a 900 rpm. Cuando se desco-
necta, la rueda sigue girando durante medio minu-
to más, hasta que se para.
a)
¿Cuál es la aceleración angular de frenado?
b)
¿Qué velocidad angular tendrá la rueda a los 20 s de
la desconexión?
Solución:
a)
−
3,14 rad/s
2
;
b)
31,4 rad/s
53
Una pelota atada a una cuerda de 1 m de radio des-
cribe círculos con una frecuencia de 10 s
−
1
en un pla-
no horizontal a una altura de 3 m sobre el suelo. Si
en cierto instante se rompe la cuerda:
a)
¿A qué distancia, medida desde la base vertical del
punto de lanzamiento, aterriza la pelota?
b)
¿Saldrá indemne un niño de 1,2 m de altura que ob-
serva el vuelo de la pelota 10 m antes del punto de
aterrizaje en el plano de la trayectoria?
Solución:
a)
49 m;
b)
Por desgracia, se llevará un certero
pelotazo a 1,11 m del suelo.
54
Un disco de vinilo gira a 33 rpm. Al desconectar el
tocadiscos, tarda 5 s en parar.
a)
¿Cuál ha sido la aceleración angular de frenado?
b)
¿Cuántas vueltas ha dado hasta pararse?
Solución:
a)
−
20,69 rad/s
2
;
b)
1,37 vueltas
55
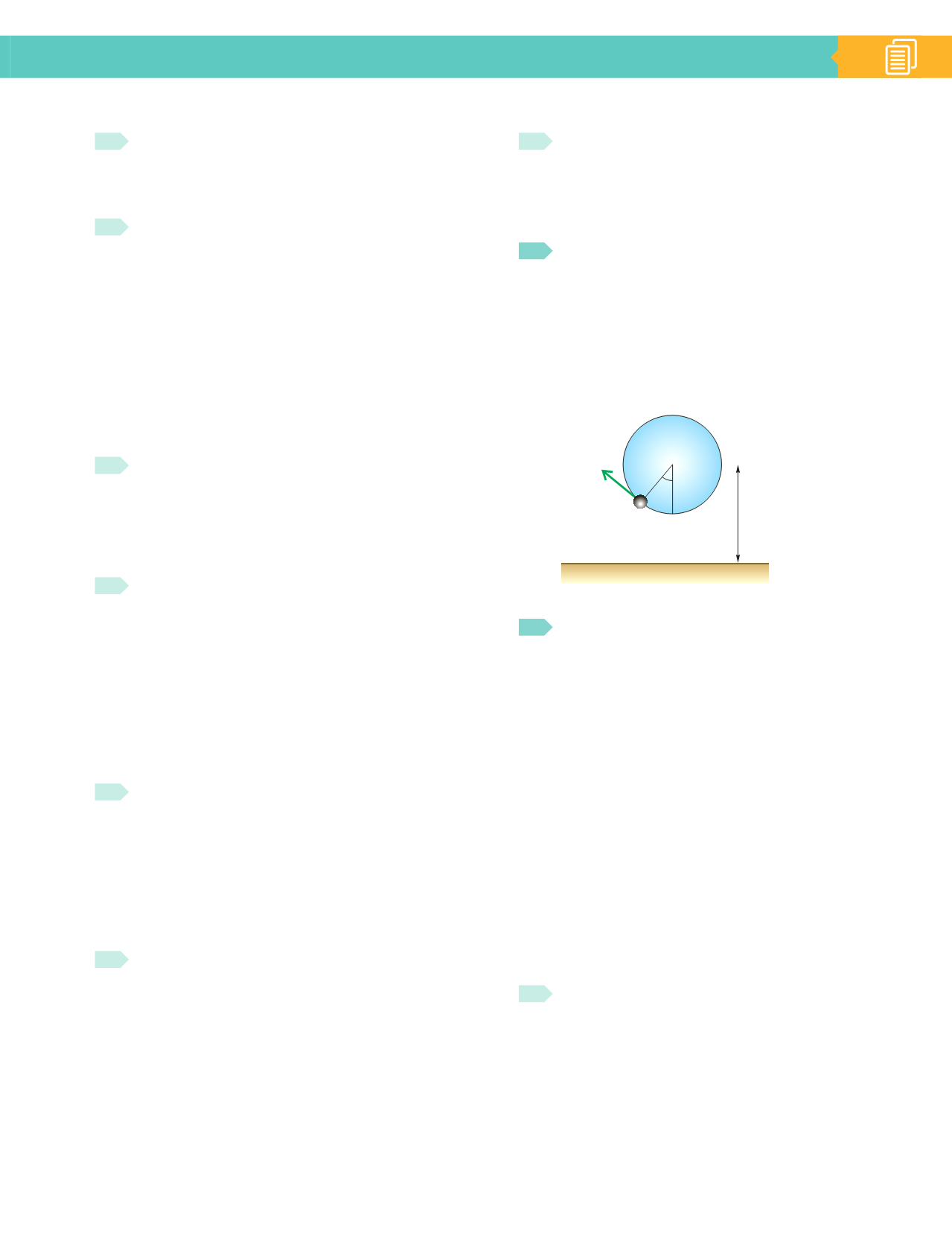
Un disco de 1 m de radio gira en un plano vertical a
300 rpm, estando su centro situado a 2 m de altura
del suelo. En su periferia lleva adherida una peque-
ña bola de acero que se despega y sale despedida
justo cuando su radio forma 40°, después de sobre-
pasar la vertical inferior, como se indica en la figura.
Determina:
a)
A qué distancia cae del suelo.
b)
A qué altura máxima asciende.
2 m
40
o
Solución:
a)
100,7 m;
b)
22 m
56
El vector de posición de un cuerpo que se mueve
con movimiento circular uniforme viene dado por la
ecuación:
r
=
4 cos(0,5
+
3
t
)
i
+
4 sen(0,5
+
3
t
)
j
m
Determina:
a)
El radio de la circunferencia.
b)
La posición angular inicial
θ
0
en radianes.
c)
El vector de posición inicial. Demuestra que su módulo
es el radio de la circunferencia.
d)
La velocidad angular, así como el período y la frecuencia.
e)
El vector velocidad en función del tiempo y su módulo.
f)
Con los datos de los apartados
a), d)
y
e),
verifica que
se cumple la relación
v
=
ω
r.
Solución:
a)
4 m;
b)
0,5 rad
c)
r
=
4 cos0,5
i
+
4sen0,5
j m;
d)
3 rad/s ; 2
π
/3 s ; 0,48 s
−
1
e)
v
=
−
12sen(0,5
+
3t )
i
+
12cos(0,5
+
3t )
j ;
v = 12 m/s
57
Un volante de 2 dm de diámetro gira en torno a su
eje a 3000 rpm; un freno lo para a 20 s. Calcula:
a)
La aceleración angular.
b)
El número de vueltas que da hasta pararse.
c)
La aceleración normal y total de un punto de su peri-
feria una vez que ha dado 100 vueltas.
Solución:
a)
−
5
π
rad/s
2
; 500 vueltas;
b)
7895,7 m/s
2
;
c)
7895,7 m/s
2


