249
Movimientos en una y dos dimensiones
ESTRATEGIAS DE RESOLUCIÓN
10
Movimientos en dos direcciones
5
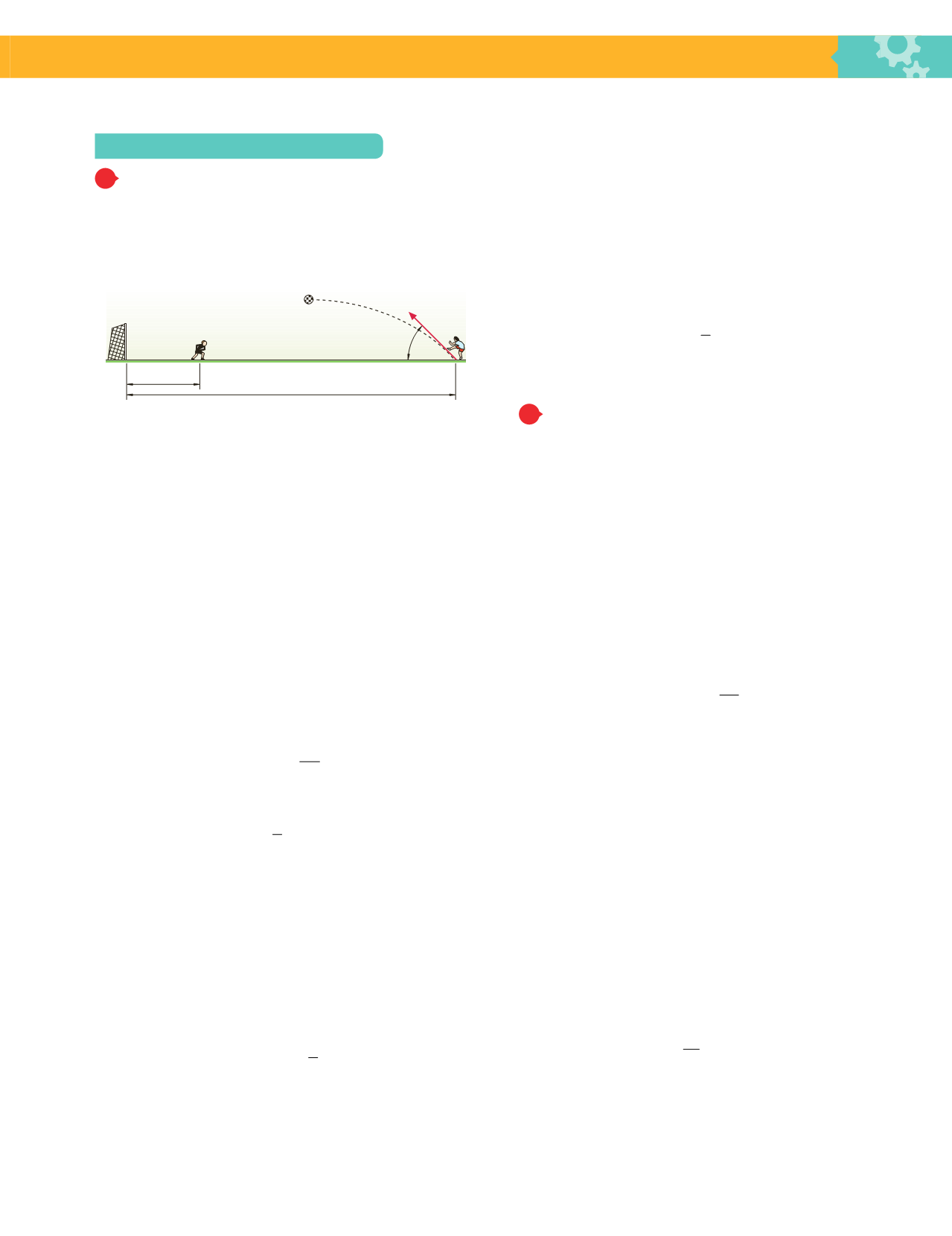
Un centrocampista trata de sorprender, desde 50 m,
a un portero adelantado, golpeando el balón en la di-
rección correcta, que sale de su bota a 80 km/h y con un
ángulo de 45° del suelo. El portero se encuentra a 7 m
de su portería y tarda 1 s en reaccionar y retroceder a
una velocidad de 2 m/s. ¿Será gol o no?
50m
7m
45º
Estrategia de resolución
No debemos presuponer ninguna circunstancia, por lo que:
1.
Primero hay que comprobar si con esa velocidad inicial (in-
cluida la dirección de 45°) el balón llega a la portería. También
podría pasarse o quedarse corto.
2.
Si llega, es necesario que lo haga por debajo del larguero
(unos 2,10 m), por lo que hay que comprobar cuál es la altura
del balón al llegar a la portería (para
x
=
50 m).
Estas dos son las condiciones iniciales para que pueda ser gol.
La
v
0
(previamente transformada a m/s) tendrá dos compo-
nentes:
v
0
x
=
v
0
cos 45°
=
15,71 m/s
v
0
y
=
v
0
sen 45°
=
15,71 m/s
Comprobamos cuál es la altura del balón cuando llega a puer-
ta (valor de
y
cuando
x
=
50 m).
El tiempo que tarda en recorrer los 50 m es:
x
=
v
0
x
t
⇒
t
=
x
v
0
x
=
3,18 s
En ese instante la altura es:
y
=
v
0
y
t
−
1
2
gt
2
=
0, 407 m
Por tanto, el balón pasa bajo los palos y puede ser gol.
3.
Nos queda por analizar la actuación del portero. Debemos
comprobar si es capaz de interceptar el balón, lo que supone
que:
❚❚
Debe existir una solución de tiempo inferior a 3,18 s en que
las posiciones del balón (
x
B
) y del portero (
x
P
) coincidan:
x
B
=
x
P
❚❚
La altura del balón en ese supuesto instante debería ser al-
canzable para un portero que corre hacia la portería.
y
=
v
0
y
t
−
1
2
gt
2
Comprobamos primero si las posiciones del balón y del portero
coinciden en un instante inferior a 3,18 s, siendo:
x
B
=
x
0B
−
x
0
x
t
=
50
−
15,71
t
x
P
=
x
0P
−
x
P
(
t
−
1)
=
7
−
2 (
t
−
1)
En la ecuación del portero se ha considerado el tiempo de
respuesta, por lo que dispone de 1 s menos.
Igualando ambas posiciones:
50
−
15,71
t
=
7
−
2(
t
−
1)
Y despejando el tiempo
t,
se obtiene:
t
=
3 s
Por consiguiente, en principio, el portero podría interceptar
el balón.
Sin embargo, la altura de este en ese instante resulta ser:
y
=
v
0
y
t
−
1
2
gt
2
=
3,03 m
Es decir, el balón resulta claramente inalcanzable para el por-
tero, que observará cómo entra en la portería.
6
Un satélite orbita a 500 km de altura sobre la superfi-
cie terrestre. Si tarda 1,57 h en dar una vuelta completa
a la Tierra, determina su velocidad angular, su velocidad
lineal y la aceleración centrípeta (en m/s
2
).
Dato: radio terrestre
=
6370 km
Estrategia de resolución
Lo primero que tenemos que hacer es establecer la velocidad
angular, lo cual es sencillo si recurrimos a la relación que guar-
da con el período.
Sin embargo, dado que la aceleración centrípeta debe expre-
sarse en m/s
2
, lo mejor es usar las unidades del sistema inter-
nacional desde el principio.
Así, tendremos:
ω
=
2
π
T
Si expresamos
T
en segundos:
T
=
1,57
⋅
3600
=
5652 s
Entonces:
ω
=
0,00111 rad/s
Puesto que
v
=
ω
r,
y dado que la conocemos, nos bastará con
determinar
r
(distancia al centro de la órbita) y expresarla en
unidades del sistema internacional.
La distancia al centro de la órbita será la suma del radio terres-
tre y la altura a la que orbita sobre la superficie.
Así pues:
r
=
R
T
+
h
=
6870 km
=
6870000 m
De este modo:
v
=
ω
r
=
7625,7 m/s
La aceleración centrípeta a la que se encuentra sometido el
satélite viene dada por:
a
c
=
v
2
r
=
8, 46 m/s
2
Comentario.
El valor de aceleración obtenido es, en realidad,
la aceleración gravitacional a que está sometido el satélite.
Respecto al porqué de la situación de ingravidez a esa altura
en el interior de una estación orbital, véase la tercera cuestión
resuelta.


