250
Unidad 10
ACTIVIDADES Y TAREAS
10
Gráficas de movimientos en una dimensión
1
¿Qué representa el área encerrada bajo una gráfica
velocidad-tiempo? ¿Por qué?
2
¿Qué representa la pendiente de la gráfica posición-
tiempo de un movimiento con velocidad constante?
3
¿Qué representa el área encerrada bajo una gráfica
aceleración-tiempo?
a)
El espacio recorrido.
b)
La velocidad.
c)
La variación de la velocidad.
4
¿Cómo determinarías la velocidad en cada instante
a partir de la gráfica posición-tiempo de un movi-
miento rectilíneo con aceleración constante?
5
Un cuerpo es lanzado verticalmente hacia arriba
con una velocidad inicial de 15 m/s. Representa sus
gráficas de movimiento (en las gráficas posición-
tiempo y velocidad-tiempo, especifica al menos los
tres puntos característicos: salida, altura máxima y
aterrizaje).
6
¿Cuál de las siguientes gráficas puede representar
mejor el módulo de la velocidad de una piedra que
se lanza verticalmente hacia arriba y cae cuando al-
canza su altura máxima?
v
t
v
t
v
t
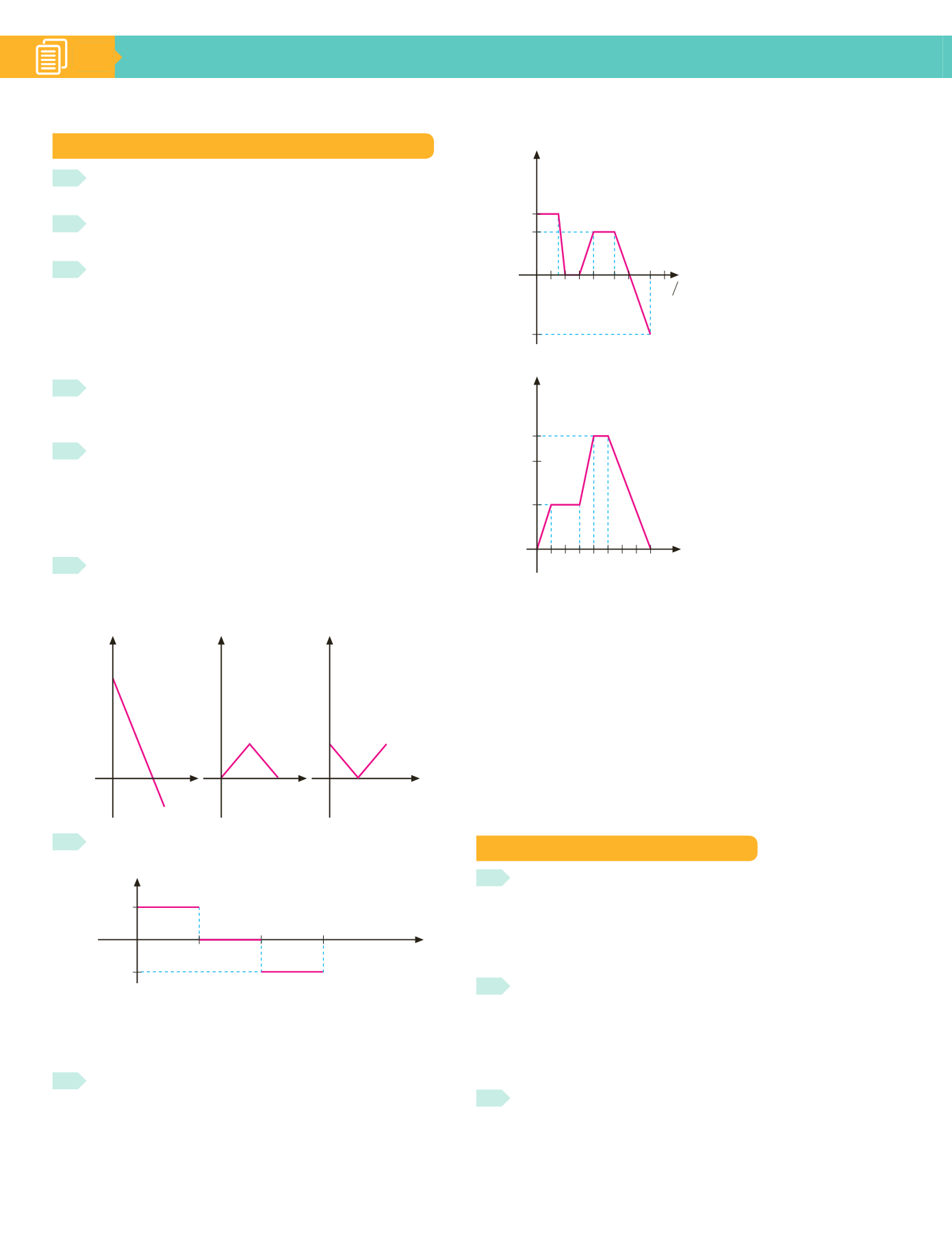
7
Una partícula inicialmente en reposo es sometida a
las aceleraciones que se muestran en la figura:
a
/(m/s )
t
/s
2
4
6
10
−
10
2
a)
Dibuja las gráficas
s-t
y
v-t.
b)
Calcula el espacio máximo recorrido a los 6 s.
Solucion:
b)
80 m
8
Interpreta las gráficas siguientes y calcula la velo-
cidad, el espacio y la aceleración en cada etapa,
así como el espacio total recorrido. Representa la
correspondiente gráfica de aceleración en cada
caso:
a)
v
/(m/s)
t
s
1 3 5 7 1012 15
?
t
/s
1 2 3 4 5 6 7 8
6,7
10
10
25
b)
v
/(m/s)
t
s
1 3 5 7 1012 15
?
t
/s
1 2 3 4 5 6 7 8
6,7
10
10
25
Solucion:
a)
tramo 0-2: v
=
10 m/s; a
=
0; s
=
20 m;
tramo 2-3: v
2
=
10 m/s; v
3
=
0; a
=
−
10 m/s
2
; s
=
5 m;
tramo 3-5: v
=
0; a
=
0; s
=
0;
tramo 5-7: v
5
=
0; v
7
=
6,7 m/s; a
=
3,35 m/s
2
; s
=
6,7 m;
tramo 7-10: v
=
6,7 m/s; a
=
0; s
=
20,1 m;
tramo 10-12: v
10
=
6,7 m/s; v
12
=
0; a
=
−
3,35 m/s
2
; s
=
6,7 m;
tramo 12-15: v
12
=
0; v
15
=
−
10,05 m/s;
a
=
−
3,35 m/s
2
; s
=
15,075 m; s
total
=
73,575 m
b)
tramo 0-1: v
0
=
0; v
1
=
10 m/s; a
=
10 m/s
2
; s
=
5 m;
tramo 1-3: v
=
10 m/s; a
=
0; s
=
20 m;
tramo 3-4: v
3
=
10 m/s; v
4
=
25 m/s; a
=
15 m/s
2
; s
=
17,5 m;
tramo 4-5: v
=
25 m/s; a
=
0; s
=
25 m;
tramo 5-8: v
5
=
25 m/s; v
8
=
0; a
=
−
8,33 m/s
2
;
s
=
37,5 m; s
total
=
105 m
Movimientos en una dimensión
9
Un movimiento que transcurre con velocidad cons-
tante puede ser:
a)
Solamente rectilíneo uniforme.
b)
Rectilíneo uniforme o circular uniforme.
Razona la respuesta.
10
Las ecuaciones del movimiento tienen que ser con-
gruentes con los resultados físicos. Si es así, las ecua-
ciones del movimiento rectilíneo con aceleración
constante, llevadas al caso en que
a
=
0, deben dar
lugar a las ecuaciones del movimiento con velocidad
constante. Demuéstralo.
11
Un protón con una velocidad inicial de 2,3
⋅
10
7
m/s
entra en una zona donde sufre una aceleración con-
traria constante de 1,3
⋅
10
15
m/s
2
. ¿Qué distancia
recorre hasta que se detiene?
Solucion:
20,3 cm


