243
Movimientos en una y dos dimensiones
Relación entre velocidad angular y lineal
Resulta evidente que existe una relación directa entre la velocidad lineal y la angular,
ya que a medida que aumenta el espacio o arco recorrido,
∆
s,
por unidad de tiempo,
también lo hace el ángulo barrido,
∆
θ
.
El módulo de la velocidad lineal es:
v
=
Δ
s
Δ
t
A partir de la definición de la posición angular, se deduce que
∆
s
=
∆
θ
r,
por lo que:
v
=
Δ
s
Δ
t
=
Δ
θ
r
Δ
t
⇒
v
=
ω
r
Ahora bien,
¿podría ser
ω
una magnitud escalar?
Resulta evidente que no, ya que la
velocidad
v
es perpendicular en todo momento al radio vector
r
, con origen en el
centro de la circunferencia (figura 10.33). Así pues,
ω
es una magnitud vectorial que
se relaciona con la velocidad lineal del siguiente modo:
v
=
ω
×
r
Recordando la definición que dimos del producto vectorial en la unidad de
Herra-
mientas matemáticas de la Física,
la dirección de
ω
es perpendicular al plano del
movimiento.
La aceleración angular
Cuando la velocidad angular de un cuerpo que se mueve describiendo círculos varía,
se dice que está dotado de
aceleración angular (
α
).
Se define la
aceleración angular
(
α
) como la
rapidez con que varía la veloci-
dad angular.
De ese modo, definida en términos de aceleración angular media:
α
=
Δ
ω
Δ
t
La
unidad de aceleración angular
en el SI es el
radián por segundo al
cuadrado (rad/s
2
).
La aceleración angular también es una magnitud vectorial. Su dirección coincide
con la de
∆
ω
.
En consecuencia, es también perpendicular al plano del movimiento.
Relación entre aceleración angular y aceleración tangencial
Teniendo en cuenta que la aceleración tangencial se define como:
a
t
=
Δ
v
Δ
t
Y, puesto que
v
= ω
r,
entonces:
a
t
=
Δ
(
ω
r
)
Δ
t
=
Δ
ω
Δ
t
r
⇒
a
t
=
α
r
Como puedes observar, es una relación directa similar a la que guardan entre sí la
velocidad lineal y la angular, y a la que guardan el espacio recorrido
s
y el ángulo
θ
(tabla 10.1).
Magnitud lineal
Magnitud angular
Relación
Espacio recorrido:
s
Ángulo barrido:
θ
s
=
θ
r
Velocidad lineal:
v
Velocidad angular:
ω
v
=
ω
r
Aceleración tangencial:
a
t
Aceleración angular:
α
a
t
=
α
r
Tabla 10.1.
Relación entre las magnitudes lineales y angulares.
Figura 10.32.
A medida que aumenta el
espacio o arco recorrido,
∆
s,
por unidad de
tiempo, también lo hace el ángulo barrido,
∆
θ
.
r
∆θ
∆
s
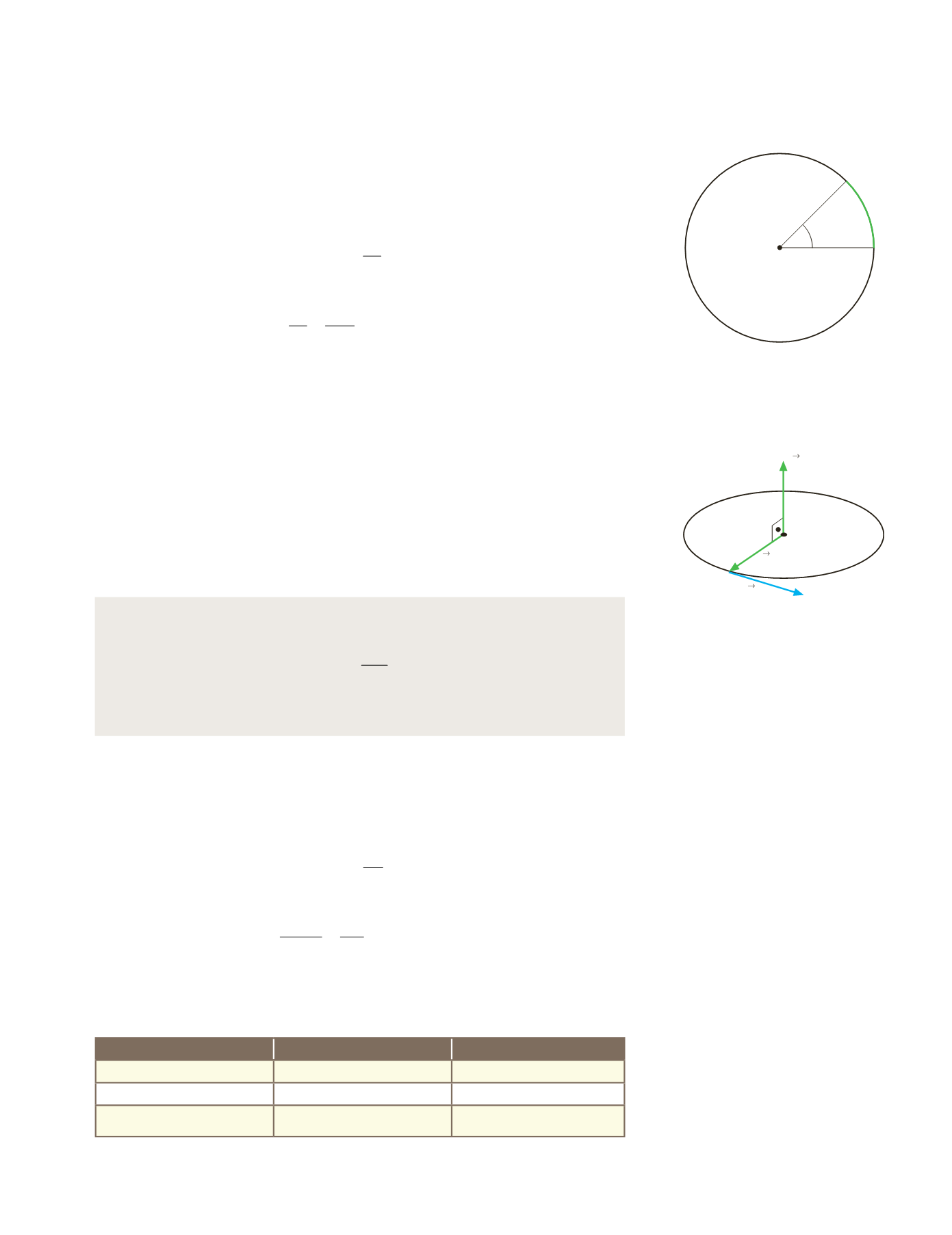
Figura 10.33.
Dirección y sentido de
ω
,
considerando el origen del sistema de
referencia en el centro de la circunferencia.
v
ω
r


