29
11
Funciones
1.
Halla el dominio, los puntos de corte con los ejes, la monotonía y los pun-
tos críticos de la función.
Dom
f
=
R
Puntos de corte con el eje
X:
(
−
2, 0), (1, 0) y (3, 0)
Puntos de corte con el eje
Y:
(0, 4)
Es creciente en (
−∞
,
−
1)
∪
(2,
+
∞
).
Es decreciente en (
−
1, 2).
Máximo: (
−
1, 3) Mínimo: (2,
−
1)
2.
Halla los puntos de corte con los ejes de coordenadas de las siguientes funciones.
a)
f
(
x
)
=
x
2
+
x
−
6
b)
f
(
x
)
=
x
+
9
a)
Puntos de corte con el eje
X
: (2, 0) y (
−
3, 0)
b)
Puntos de corte con el eje
X
: (
−
9, 0)
Puntos de corte con el eje
Y:
(0,
−
6)
Puntos de corte con el eje
Y:
(0, 3)
3.
Representa gráficamente una función que cumpla todas las característi-
cas indicadas.
❚
Dom
f
=
[
−
2, 5]
❚
Tiene un máximo en (2, 2).
❚
Pasa por el origen de coordenadas.
❚
Corta al eje
X
en (4, 0).
4.
Clasifica las siguientes funciones según su simetría.
a)
f
(
x
)
=
x
3
−
6
x
b)
f
(
x
)
=
x
6
−
6
a)
f
(
−
x
)
=
(
−
x
)
3
−
6(
−
x
)
=
−
x
3
+
6
x
b)
f
(
x
)
=
x
6
−
6
−
f
(
x
)
=
−
(
x
3
−
6
x
)
=
−
x
3
+
6
x
f
(
−
x
)
=
(
−
x
)
6
−
6
=
x
6
−
6
La función tiene simetría impar.
La función tiene simetría par.
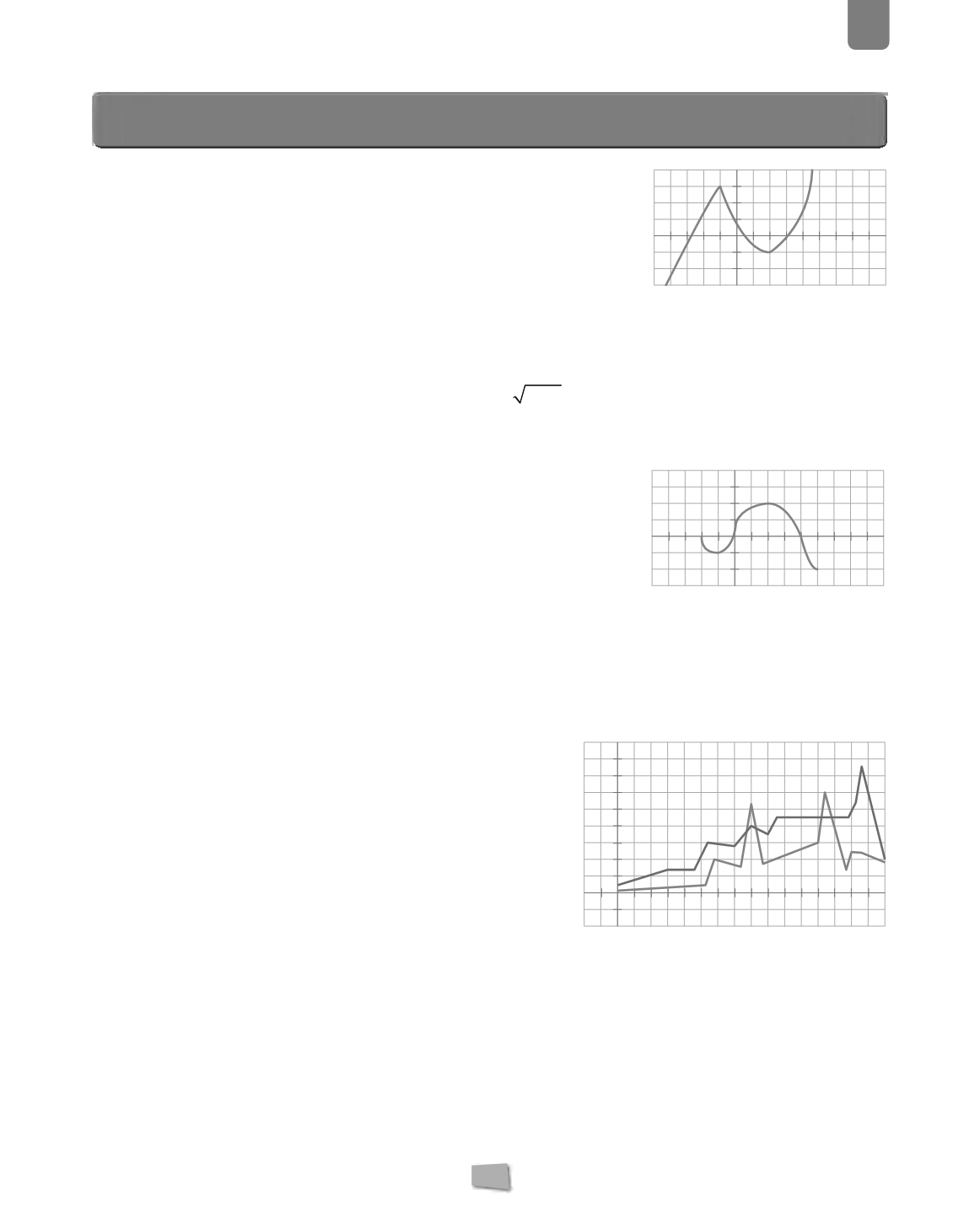
5.
La gráfica representa los niveles de audiencia de dos cadenas
televisivas desde las 7 h a las 24 h, en un día cualquiera de pro-
gramación.
Responde razonadamente.
a)
¿Qué cadena es la que tiene mayor audiencia?
b)
Teniendo en cuenta que las noticias se emiten a las 15 h y las
21 h, ¿qué cadena prefieren los telespectadores para infor-
marse?
c)
¿En qué cadena y a qué hora se emite el programa de mayor audiencia?
d)
El número de telespectadores se mantiene constante en una cadena y en un tramo horario. Di cuál es la
cadena en la que ocurre esto y cuál es el tramo.
a)
La cadena A.
b)
La cadena B.
c)
En la cadena A, a las 23 h.
d)
En la cadena A, entre las 17 h y las 22 h.
PROPUESTA DE EVALUACIÓN
PRUEBA B
O
1
1
Y
X
8
500
O
Espectadores
Tramo horario
A
B
O
1
1
Y
X


