11
Funciones
20
38
Dadas las funciones:
I
f
(
x
)
=
x
−
1
II
f
(
x
)
=
x
2
−
1
III
f
(
x
)
=
2
x
IV
f
(
x
)
=
1
x
−
3
a)
Calcula los valores
f
(
−
1),
f
(0) y
f
(3), en cada una.
b)
Halla también el dominio de cada función.
a)
•
f
(
x
)
=
x
−
1
f
(
−
1)
=
−
2,
f
(0)
=
−
1 y
f
(3)
=
2
•
f
(
x
)
=
x
2
−
1
f
(
−
1)
=
0,
f
(0)
=
−
1 y
f
(3)
=
8
•
f
(
x
)
=
2
x
f
(
−
1) no tiene sentido calcularlo, ya que
−
1 no pertenece al dominio de la función.
f
(0)
=
0 y
f
(3)
=
6
•
f
(
x
)
=
1
x
−
3
→
f
(
−
1)
=
1
−
4
f
(0)
=
1
−
3
f
(3) no tiene sentido calcularlo, ya que 3 no pertenece al dominio.
b)
f
(
x
)
=
x
−
1 Dom
f
=
R
f
(
x
)
=
2
x
Dom
f
=
[0,
+
∞
)
f
(
x
)
=
x
2
−
1 Dom
f
=
R
f
(
x
)
=
1
x
−
3
→
f
(
−
1)
=
1
−
4
f
(0)
=
1
−
3
Dom
f
=
R
−
{3}
39
Determina los puntos de corte con los ejes de estas funciones.
a)
b)
O
1
1
X
Y
O
1
1
X
Y
a)
(
−
1, 0), (2, 0) y (0,
−
4)
b)
(
−
1, 0), (1, 0), (3, 0) y (0, 3)
40
Halla los puntos de corte con los ejes de las funciones.
a)
f
(
x
)
=
x
−
1
b)
f
(
x
)
=
x
2
−
9
c)
f
(
x
)
=
x
−
1
2
d)
f
(
x
)
=
x
2
−
x
−
12
a)
Con el eje
X
: (1, 0)
b)
Con el eje
X
: (3, 0)
c)
Con el eje
X
: (1, 0)
d)
Con el eje
X
: (4, 0)
y (
−
3, 0)
y (
−
3, 0)
Con el eje
Y
: (0,
−
1) Con el eje
Y
: (0,
−
9) Con el eje
Y
:
0,
−
1
2
⎛
⎝
⎜⎜⎜
⎞
⎠
⎟⎟⎟
Con el eje
Y
: (0,
−
12)
41
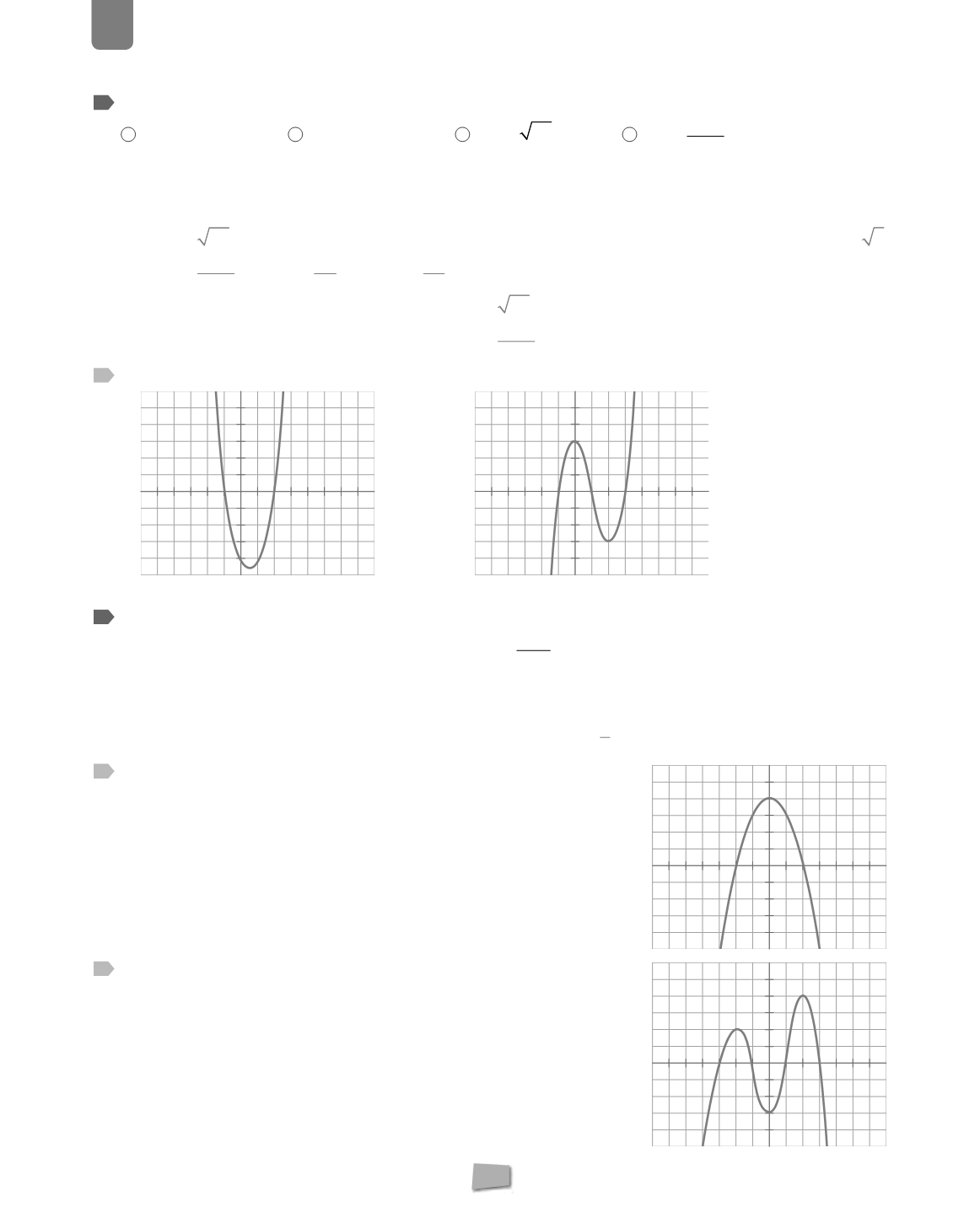
Estudia la continuidad y la monotonía de la función representada en esta gráfica.
¿Cuáles son los máximos y los mínimos de esta función?
Es una función continua.
Es creciente en el intervalo (
−∞
, 0) y decreciente en (0,
+
∞
).
Tiene un punto máximo, el (0, 4) y no tiene puntos mínimos.
42
Indica los intervalos de crecimiento y decrecimiento, así como los extremos rela-
tivos de esta función.
Es creciente en (
−∞
,
−
2) y (0, 2) y decreciente en (
−
2, 0) y (2,
+
∞
).
Tiene dos puntos máximos: (
−
2, 2) y (2, 4) y un punto mínimo, el (0,
−
3).
O
1
1
X
Y
O
1
1
X
Y


