223
En general, para calcular la función inversa,
f
1
(
x
), de una función inyec-
tiva,
f
(
x
), el procedimiento es el siguiente:
Se hace que
f
(
x
)
y.
Se intercambian
x
e
y.
Se despeja
y
en función de
x.
Ejercicio resuelto
Dada la función inyectiva f
(
x
)
1
x
2
x
, hallar f
1
(
x
)
.
Procedemos del siguiente modo:
Se hace que
f
(
x
)
y:
y
1
x
2
x
Se intercambian
x
e
y:
x
1
y
2
y
Se despeja
y
en función de
x:
x y
1 2
y
⇒
x y
2
y
1
(
x
2)
y
1
⇒
y
x
1
2
Por tanto, podemos concluir que:
f
1
(
x
)
x
1
2
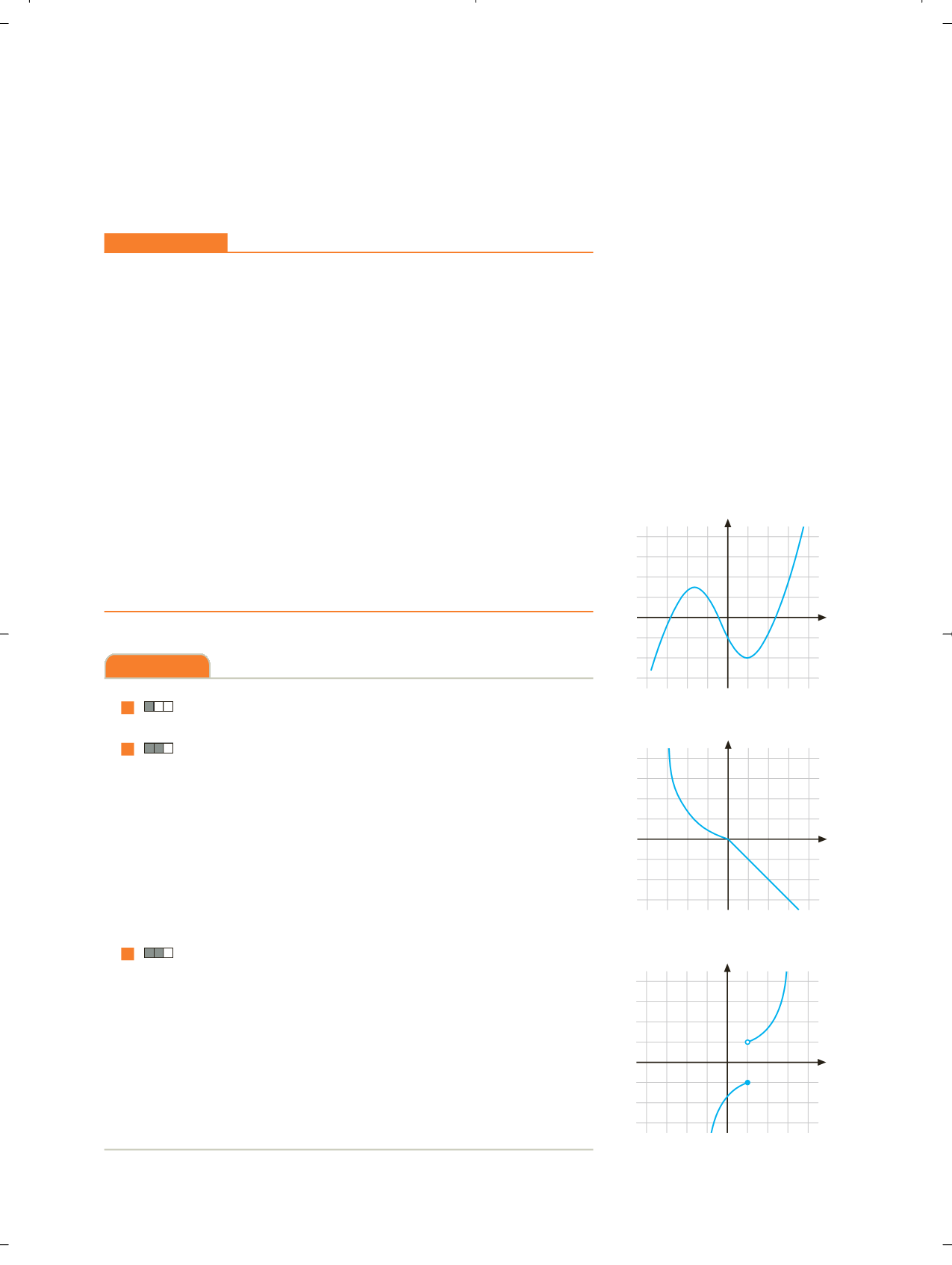
Indica qué tipo de funciones representan las gráficas de las figuras 8.36:
inyectivas, suprayectivas o biyectivas.
Indica cuáles de estas funciones son inyectivas:
a)
f
(
x
)
1
x
2
b)
f
(
x
)
x
2
2
x
3
c)
f
(
x
)
3
2
4
x
d)
f
(
x
)
x
3
2
e)
f
(
x
)
2
x
2
x
7
f)
f
(
x
)
x
1
Calcula la función inversa,
f
1
(
x
), de las siguientes funciones:
a)
f
(
x
)
1
6
3
x
b)
f
(
x
)
2
3
2
x
c)
f
(
x
)
7
x
x
d)
f
(
x
)
3
x
2
e)
f
(
x
)
4
3
5
x
x
18
17
16
Actividades
▼
Y
X
O
Y
X
O
X
Y
O
F
IGURA
8.36.a.
F
IGURA
8.36.b.
F
IGURA
8.36.c.


