205
2.
Representación gráfica
de una función
Dado que una función,
f:
, es una aplicación, está constituida por
un conjunto de pares ordenados de elementos de , (
x, f
(
x
)). Estos pares de
números se pueden representar en un sistema de coordenadas cartesianas
mediante puntos, (
x, y
), donde
y f
(
x
).
Si la función está expresada de la forma
y f
(
x
), asignando valores a
x,
se
pueden obtener pares de números, (
x, f
(
x
)). Cuantos más pares de números
tengamos, más detallada será la representación gráfica de la función.
Si la función viene definida por una tabla de valores, se representa la
variable independiente en el eje de abscisas y la dependiente en el de ordena-
das, con lo que se obtiene un conjunto de puntos que constituyen su repre-
sentación gráfica.
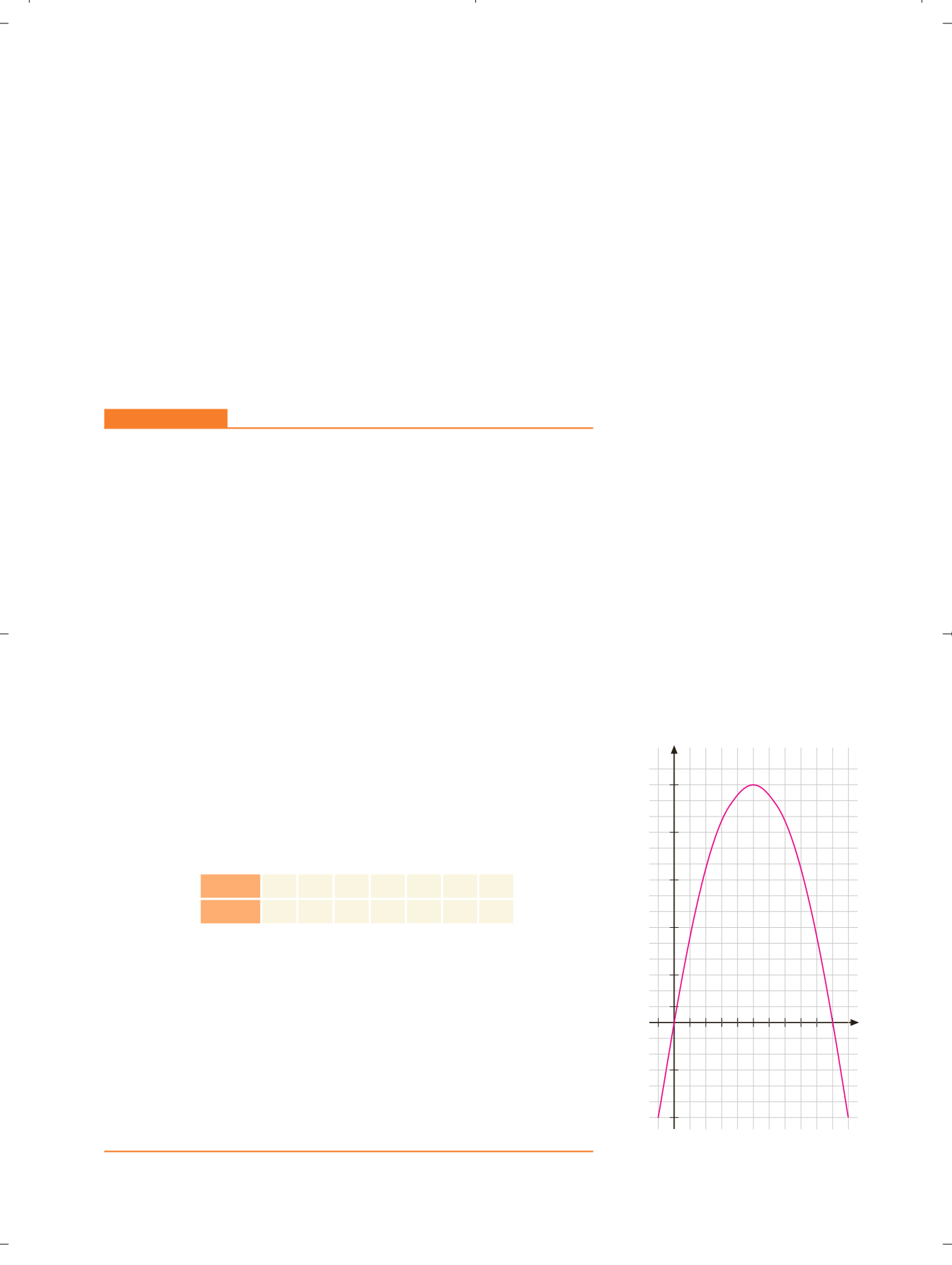
Ejercicio resuelto
Representar la función f(x) (
1/2
)x
2
10
x. (La expresión de esta fun-
ción es la misma que la obtenida en el primer ejemplo del epígrafe anterior.)
Como puedes observar, se trata de una función polinómica de segundo gra-
do. Para realizar su representación gráfica (una parábola) es preciso deter-
minar las coordenadas de su vértice y los puntos en los que la gráfica corta
al eje de abscisas, así como completar un cuadro de valores con algunos
puntos más, dispuestos de forma simétrica respecto de la abscisa del vértice.
En nuestro caso,
a
1/2,
b
10 y
c
0.
El vértice se determina de la siguiente forma:
x
v
2
a
b
2 (
1
1
0
/2)
10
y
v
( 1/2) 10
2
10 10 50
Por tanto, el vértice se encuentra en el punto (10, 50).
Los puntos en los que la gráfica corta al eje de abscisas son los que tienen la
ordenada igual a cero,
y
0. Es decir, hemos de calcular para qué valores
de
x
se anula
f
(
x
):
f
(
x
) 0
⇒
(1/2)
x
2
10
x
0
⇒
(( 1/2)
x
10)
x
0
⇒
⇒
x
0 y ( 1/2)
x
10 0
Así pues, la gráfica corta al eje de abscisas en
x
0 y
x
20.
Por último, construimos una tabla de valores y representamos los puntos:
El dominio es Dom
f
.
Para establecer el recorrido, se observa que, como
a
1/2 0, la parábola
es convexa, por lo que el
vértice,
(10, 50), es el punto cuya ordenada,
y
50
,
constituye el valor
máximo
que toma la función.
Esto quiere decir que Rec
f
(
∞
, 50].
En el contexto del primer ejemplo del epígrafe anterior, esto significa que el
área máxima que puede tener el triángulo que se indicaba es de 50 cm
2
. Ade-
más, si
x,
que es la altura y, por tanto, ha de ser positiva, tomara valores mayo-
res que 20 cm, el área sería negativa, como se observa en la gráfica, lo cual es
absurdo, por lo que el dominio de la función área es el intervalo real (0, 20).
▼
x
y f
(
x
)
2
22
0
0
6
42
10 14 20
50 42
0
22
22
Y
42
10
86 10 12 14 16 18 20
20
30
40
50
X
10
20
O
f
(
x
)
( 1/2)
x
2
10
x
F
IGURA
8.1.


