215
5.3.
Concavidad y convexidad
Una función,
f
(
x
), es
cóncava
en un intervalo si para cualquier par de
puntos del intervalo, el segmento que los une queda por encima de la grá-
fica de
f
(
x
) en dicho intervalo (figura 8.20.a).
Para cualquier valor
x
(
a, b
), se cumple que:
f
(
b
b
)
f
a
(
a
)
f
(
x
x
)
f
a
(
a
)
Esta característica geométrica define el intervalo en que
f
(
x
) es cóncava.
Una función,
f
(
x
)
,
es
convexa
en un intervalo si para cualquier par de
puntos del intervalo, el segmento que los une queda por debajo de la gráfi-
ca de
f
(
x
) en ese intervalo (figura 8.20.b).
Se debe cumplir que
∀
x
(
a
,
b
):
f
(
b
b
)
f
a
(
a
)
f
(
x
x
)
f
a
(
a
)
Observa ahora estas figuras:
F
IGURA
8.21.a.
F
IGURA
8.21.b.
Se hace patente que, si una función es cóncava en un determinado inter-
valo, queda por encima de las rectas tangentes que se pueden trazar en cual-
quiera de sus puntos. Cuando una función es convexa queda por debajo de
cada una de sus rectas tangentes en dicho intervalo.
En ocasiones, hay puntos de la gráfica de la función en que la recta tangen-
te atraviesa la curva: a un lado del punto la tangente queda, por ejemplo, por
debajo de la gráfica, y, por el otro, queda por encima (figura 8.22). Esto signi-
fica que a un lado la función es cóncava, y al otro lado convexa.
Se dice que (
a
,
f
(
a
)) es un
punto de inflexión
de
f
(
x
) si en él se produce
un cambio en la curvatura de la función.
Ejercicio resuelto
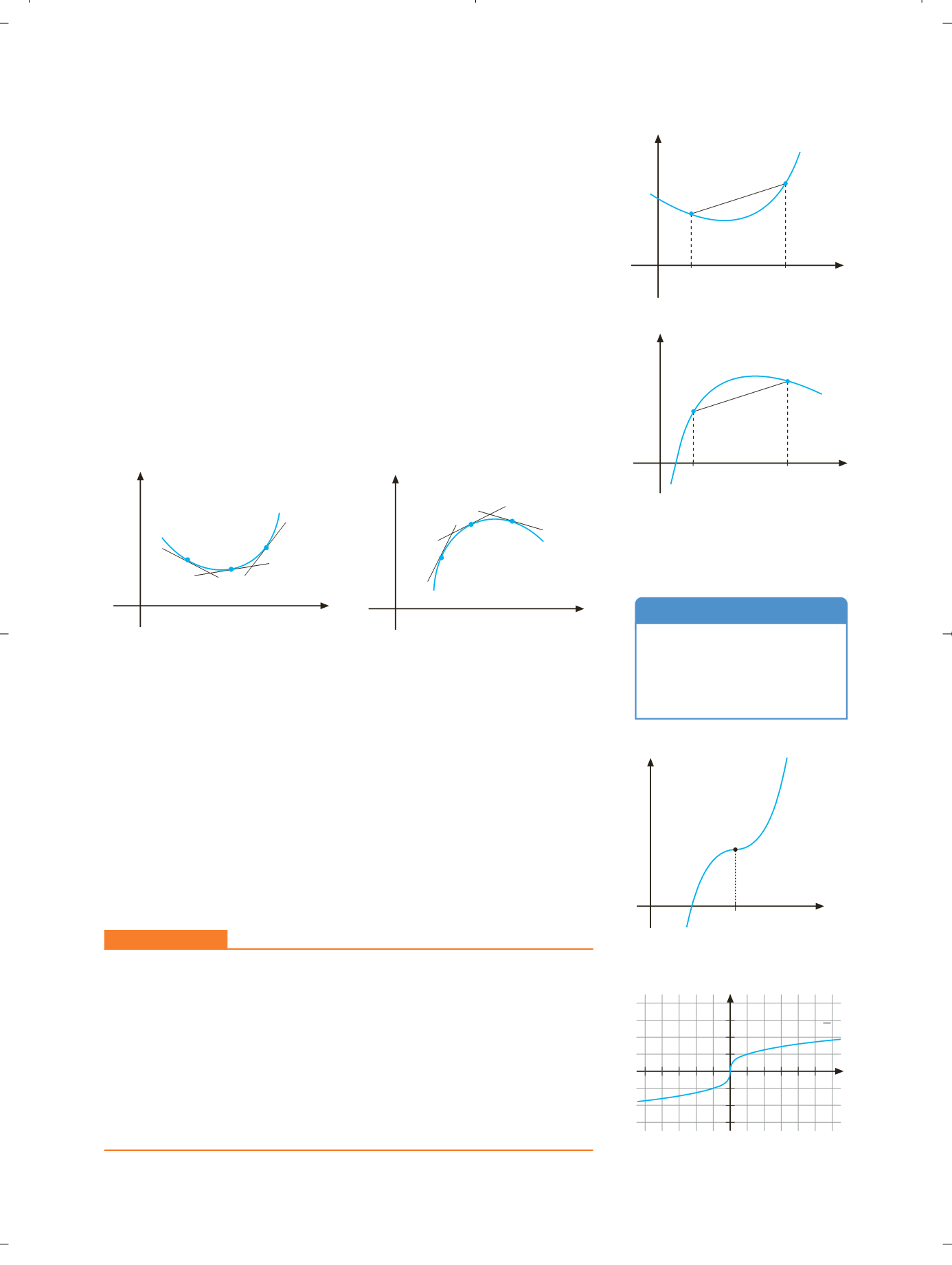
Determinar los intervalos de concavidad y convexidad de la función:
f
(
x
)
3
x
H
allar, si los tiene, sus puntos de inflexión.
Esta función es continua en todo el conjunto .
En (
∞
, 0),
f
(
x
) es cóncava.
En (0,
∞
),
f
(
x
) es convexa.
Por lo tanto, en el punto (0, 0) la función tiene un punto de inflexión.
▼
O
Y
X
O
Y
X
O
Y
X
b
a
(
a
,
f
(
a
))
(
b
,
f
(
b
))
O
Y
X
b
a
(
a
,
f
(
a
))
(
b
,
f
(
b
))
F
IGURA
8.20.a.
F
IGURA
8.20.b.
OBSERVA
Una función que posea un míni-
mo en un determinado entorno
es cóncava en ese entorno. Y si
posee un máximo, entonces en su
entorno es convexa.
X
Y
O
a
f
f’’
(
a
)
0
convexa
cóncava
F
IGURA
8.22.
O
1
1
Y
2
3
2 3 4 5
1
2
3
X
3 5
f
(
x
)
3
√
x
F
IGURA
8.23.


