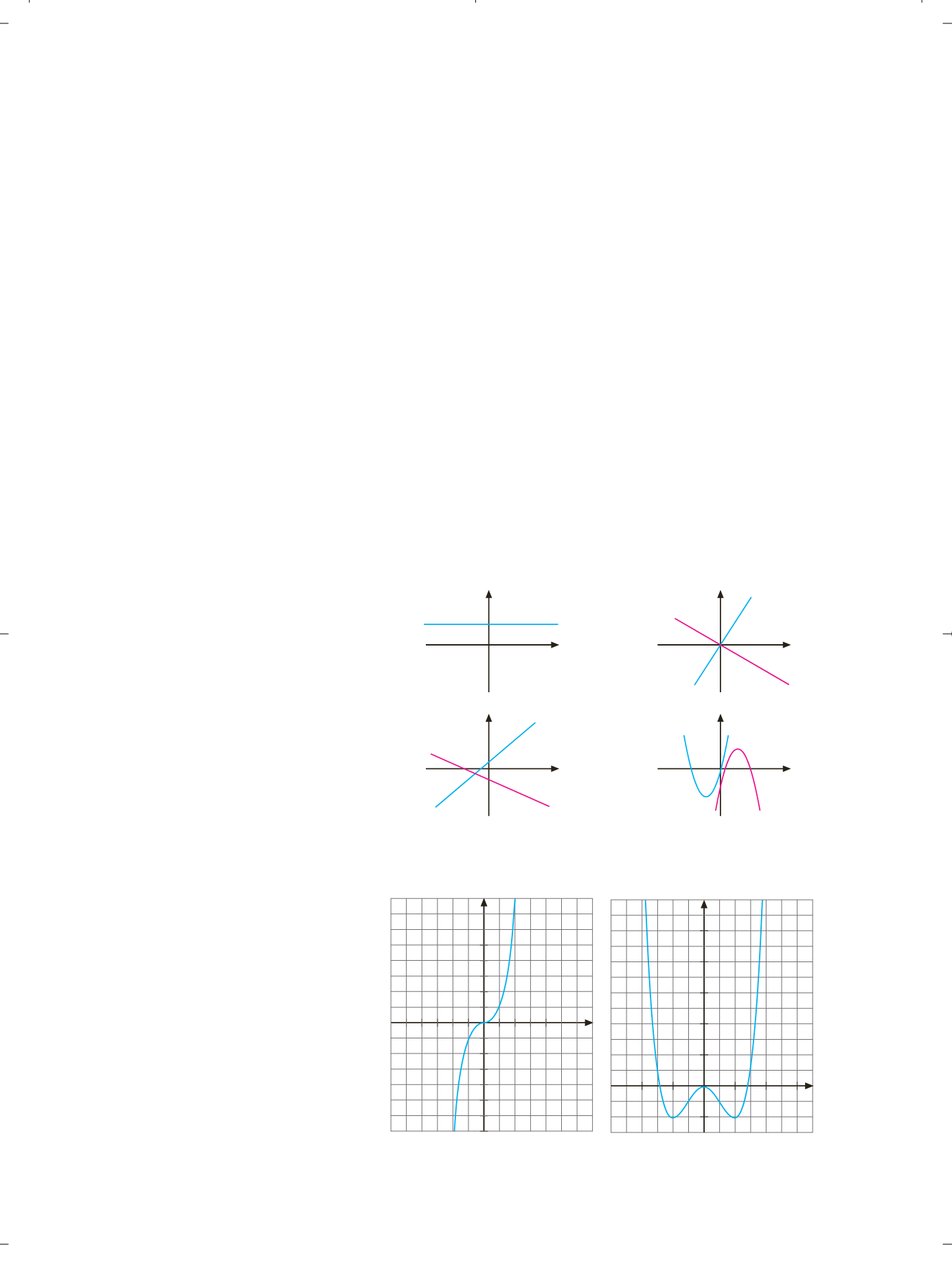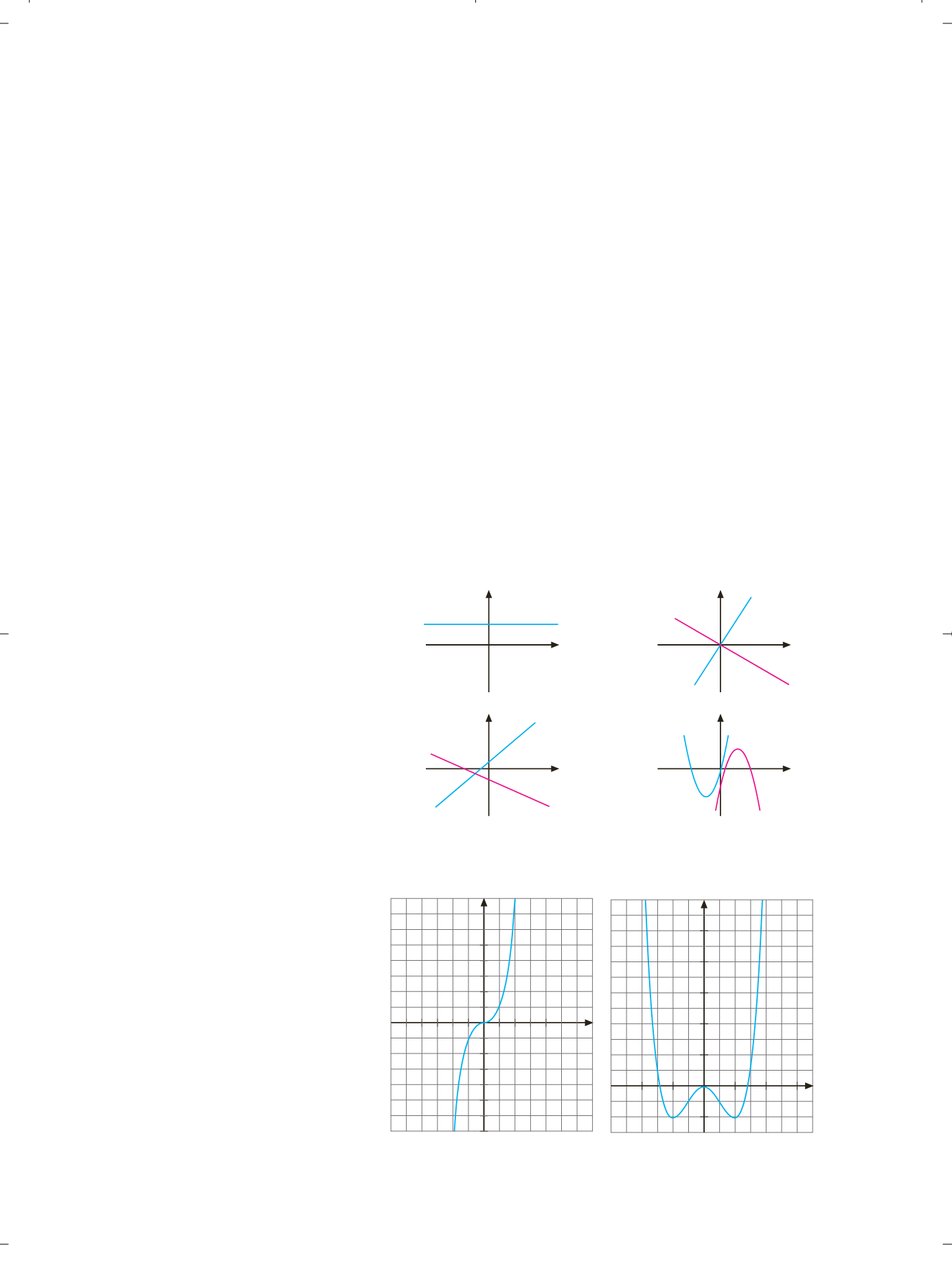
208
3.
Cálculo del dominio de una función
Son
funciones algebraicas
aquellas cuya variable independiente,
x,
está
sometida a operaciones algebraicas: suma, resta, multiplicación, división,
potenciación y radicación. Todas las funciones polinómicas, racionales e irra-
cionales son algebraicas.
Las funciones que no son algebraicas, se denominan
trascendentes.
Las
funciones logarítmicas, exponenciales y trigonométricas son trascendentes.
3.1.
Funciones polinómicas
Las
funciones polinómicas
son todas aquellas cuya expresión es la de un
polinomio:
f
(
x
)
p
0
p
1
x p
2
x
2
…
p
n
2
x
n
2
p
n
1
x
n
1
p
n
x
n
En estas funciones, cualquier número real,
x
, tiene imagen. Es decir,
al sustituir
x
por un número real cualquiera en la expresión anterior, siempre
existe
f
(
x
). Por tanto, el dominio de todas estas funciones polinómicas es .
Así, el dominio de la función polinómica
f
(
x
) 4
x
5
3
x
2
x
1 es .
Las funciones polinómicas más conocidas son:
La función constante,
f
(
x
)
k.
La función de proporcionalidad directa,
f
(
x
)
kx.
La función lineal,
f(x) ax b.
La función cuadrática,
f
(
x
)
ax
2
bx c
.
F
IGURA
8.8.a.
A continuación se muestran las representaciones de algunas funciones polinó-
micas de órdenes superiores:
f
(
x
)
x
3
(figura 8.8.b) y
g
(
x
)
x
4
2
x
2
(figura 8.8.c).
F
IGURA
8.8.b.
F
IGURA
8.8.c.
Y
X
Y
X
Y
X
Y
X
f
(
x
)
ax b
a
0
a
0
f
(
x
)
kx
k
0
k
0
f
(
x
)
ax
2
bx
c
a
0
a
0
f
(
x
)
k
O
O
O
O
1 2 3 4 5
12345
1
2
3
4
5
2
3
4
5
6
f
(
x
)
x
3
Y
X
g
(
x
)
x
4
2
x
2
1 2 3
1 2
1
2
3
1
4
5
X
Y