213
5.
Características de una función
5.1.
Signo de una función
Dada una función,
f
(
x
), determinar su signo es hallar para qué valores de
su dominio es
f
(
x
) 0 y
f
(
x
) 0.
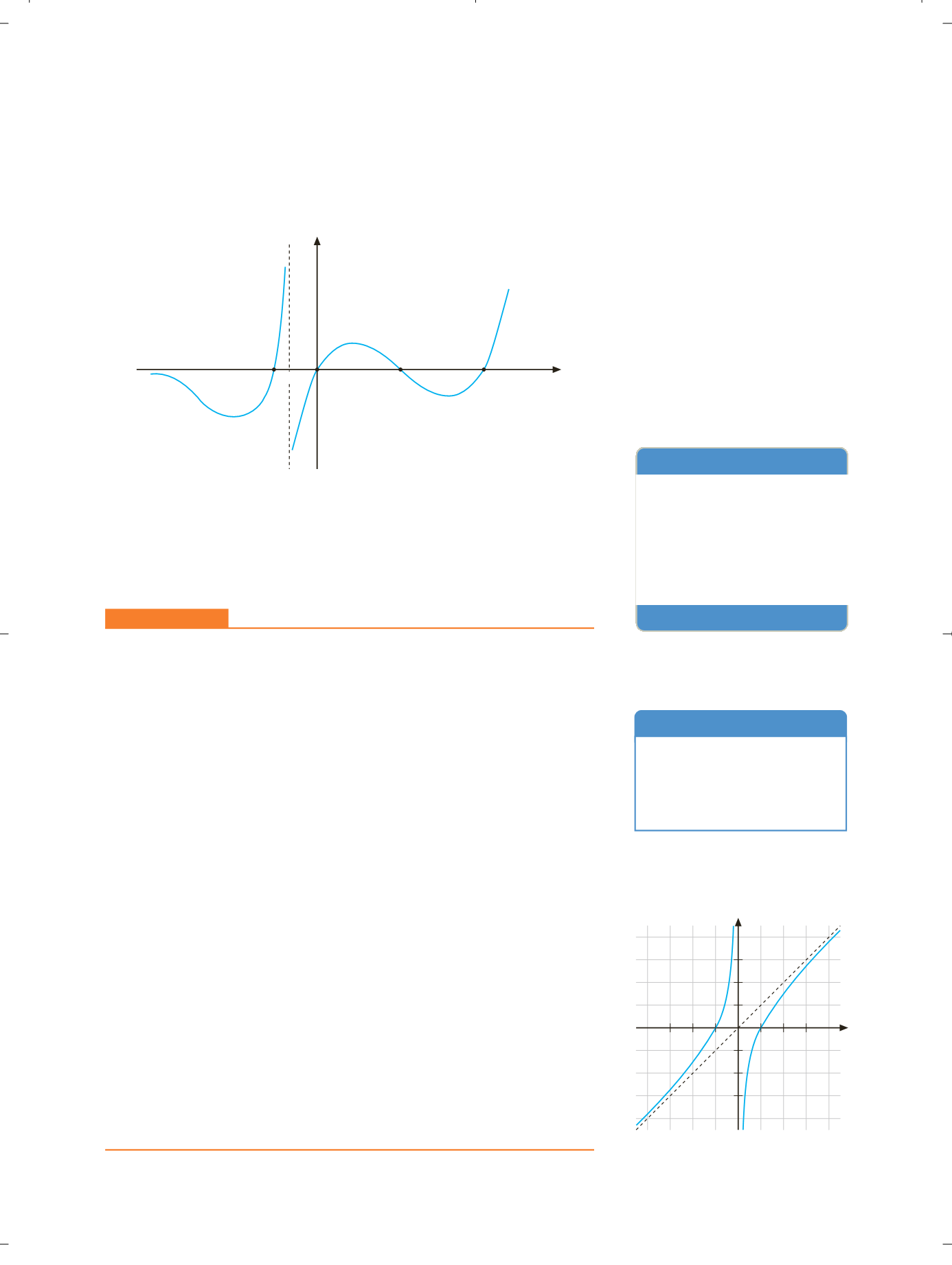
F
IGURA
8.15.
A partir de su representación gráfica,
f
(
x
) 0 para el conjunto de puntos
situados por encima del eje de abscisas, y
f
(
x
) 0 para aquellos puntos que
se hallan por debajo. A partir de su expresión analítica, es preciso encontrar
los posibles cambios de signo, determinando los ceros de la función y los puntos
en los que no está definida. Con estos datos se pueden establecer los intervalos
de signo constante.
Ejercicio resuelto
Determinar los intervalos de signo constante en el dominio de esta función:
f
(
x
)
x
4
x
Hay que averiguar los ceros de
f
(
x
):
f
(
x
) 0 si
x
4
x
0, esto es, si
x
2
4 0
Por tanto, para
x
2 y para
x
2 la función se anula.
También hay que hallar los puntos en los que la función no existe.
Dado que
x
4
x
no existe para
x
0, no existe
f
(0); por tanto:
Dom (
f
)
{0}
A continuación, se deducen los intervalos de signo constante, que son:
(
∞
, 2), ( 2, 0), (0, 2) y (2,
∞
)
Para cada intervalo se halla el signo de la imagen de un punto interior cual-
quiera, y ese signo es el de todas la imágenes que corresponden a ese intervalo:
f
( 3)
3
4
3
0
⇒
f
(
x
) 0
∀
x
(
∞
, 2)
f
( 1)
1
4
1
0
⇒
f
(
x
) 0
∀
x
( 2, 0)
f
(1) 1
4
1
0
⇒
f
(
x
) 0
∀
x
(0, 2)
f
(3) 3
4
3
0
⇒
f
(
x
) 0
∀
x
(2,
∞
)
Observa la gráfica de esta función en la figura 8.16 y comprueba los resultados.
▼
F
IGURA
8.16.
Y
X
O d
a
b
c
Dom (
f
)
{
a
}
f
(
x
)
0 si
x
{
d, O, b, c
}
X
Y
6 4
2 4 6
6
4
2
4
6
2
2
f
(
x
)
x
4
x
O
OBSERVA
Si una función se puede
factorizar, para averiguar sus in-
tervalos de signo constante es
conveniente construir su cuadro
de signos.
Ceros de una función
Son ceros de una función los
valores del dominio que satisfacen
f
(
x
) 0, es decir, las soluciones de la
ecuación
f
(
x
) 0.
Los puntos en los que la función no
está definida son aquellos que no per-
tenecen al dominio,
x
Dom (
f
).


