209
X
O
Y
f
(
x
)
1/
x
1 2 3 4
1
2
3
4
1
2
3
4
2 1
3 4
F
IGURA
8.9.
X
O
Y
1
2
3
1 2 3 4
2
5
4
F
IGURA
8.10.
∞
1
3
∞
x
1
3
x
(
x
1) (3
x
)
3.2.
Funciones racionales
Las
funciones racionales
son aquellas cuya expresión es una fracción alge-
braica, es decir, el cociente entre dos polinomios:
f
(
x
)
p
q
(
(
x
x
)
)
El dominio de este tipo de funciones está formado por aquellos valores
reales que no anulan el denominador. En general, se puede escribir:
Dom
f
{
x
⏐
q
(
x
) 0}
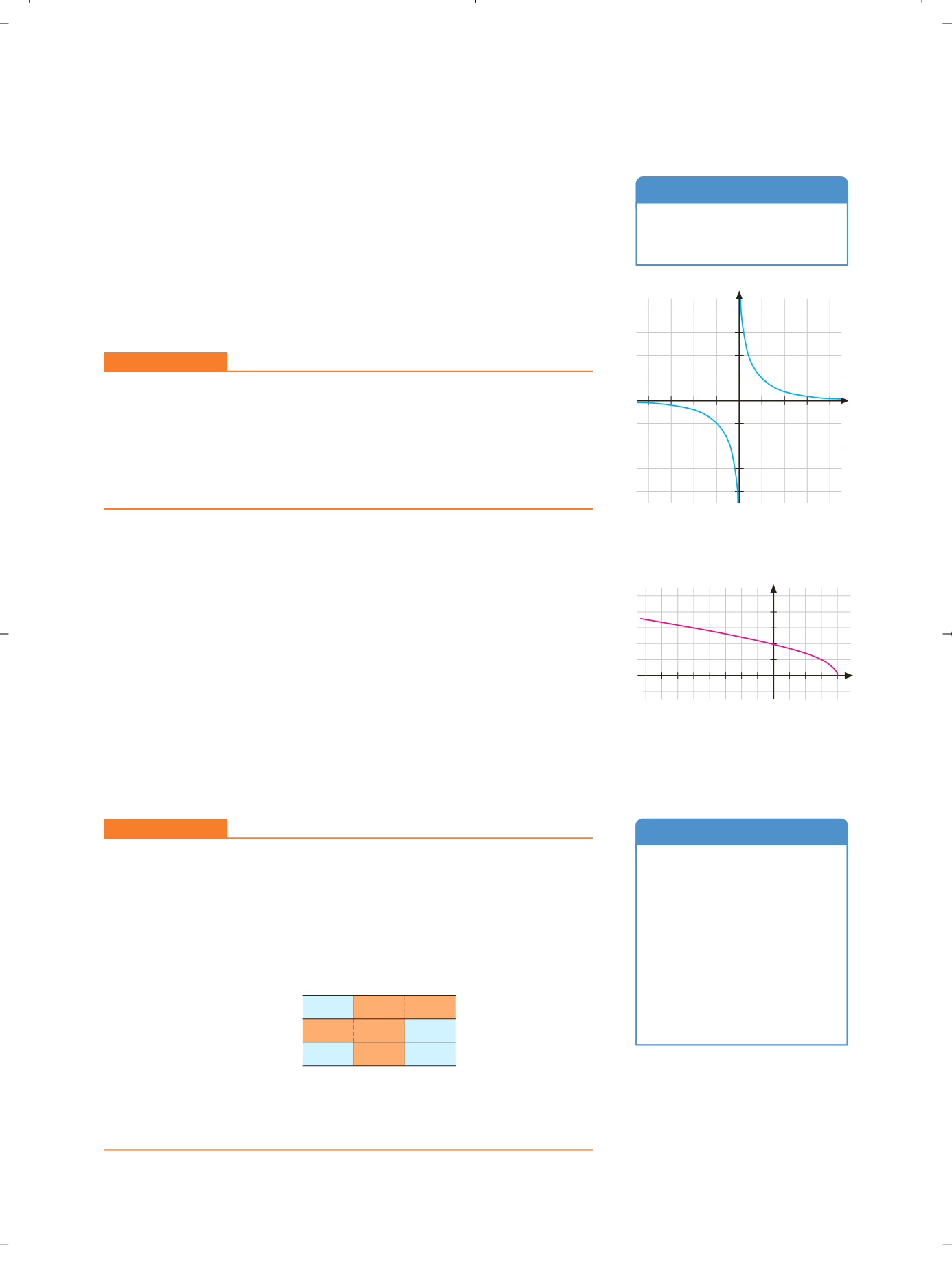
Un ejemplo de función racional es la función de proporcionalidad inversa,
f
(
x
) 1/
x
(figura 8.9), cuyo dominio es
{0}.
Ejercicio resuelto
Hallar el dominio de f
(
x
)
3
x
x
2
1
1
.
Dom
f
{
x
⏐
x
2
1 0}
Dado que
x
2
1 0 para
x
1 y
x
1, resulta:
Dom
f
{ 1, 1} (
∞
, 1) ( 1, 1) (1,
∞
)
3.3.
Funciones irracionales
Las
funciones irracionales
son aquellas cuya expresión matemática
presenta un radical
n
g
(
x
), donde
g
(
x
) es una función polinómica o racional.
Dada
f
(
x
)
n
g
(
x
), si el índice de la raíz,
n,
es par, el dominio de la
función son los valores de
x
que hacen que el radicando sea positivo o nulo. Sin
embargo, si
n
es impar, el dominio de
f
(
x
) es el mismo que el de
g
(
x
).
El dominio de
f
(
x
)
4
x
es {
x
⏐
4
x
0}.
Así, 4
x
0 si
x
4, esto es,
x
4, por lo que Dom
f
(
∞
, 4].
El dominio de
f
(
x
)
3
x
x
1
es {
x
⏐
x
0}
{0}.
Ejercicio resuelto
Hallar el dominio de f
(
x
)
x
2
2
x
3.
Dom
f
{
x
⏐
x
2
2
x
3 0}
Dado que
x
2
2
x
3 (
x
1) (3
x
), hay que determinar para qué
valores de
x
el producto de estos factores es mayor o igual que cero. Para
ello, es útil realizar un cuadro de signos como el que sigue:
Como se observa, el producto es positivo o nulo en el intervalo [ 1, 3].
Por tanto:
Dom
f
{
x
⏐
1
x
3} [ 1, 3]
▼
▼
OBSERVA
Para designar un subconjunto de
números reales, puede usarse
también la notación de intervalo.
OBSERVA
Los
cuadros de signos
son úti-
les siempre que la función pueda
descomponerse en productos o
cocientes de productos, y siempre
que sea posible determinar sus
ceros y los puntos en los que no
esté definida.
Para descomponer una función
polinómica,
f
(
x
), se utiliza la regla
de Ruffini, o, si es de segundo gra-
do, se resuelve la ecuación
f
(
x
) 0.


