212
4.
Cálculo del recorrido
de una función
Dada una función,
f
(
x
), el conjunto de valores reales,
y
, que poseen
antiimagen, es decir,
y f
1
(
x
), constituye el recorrido de dicha función.
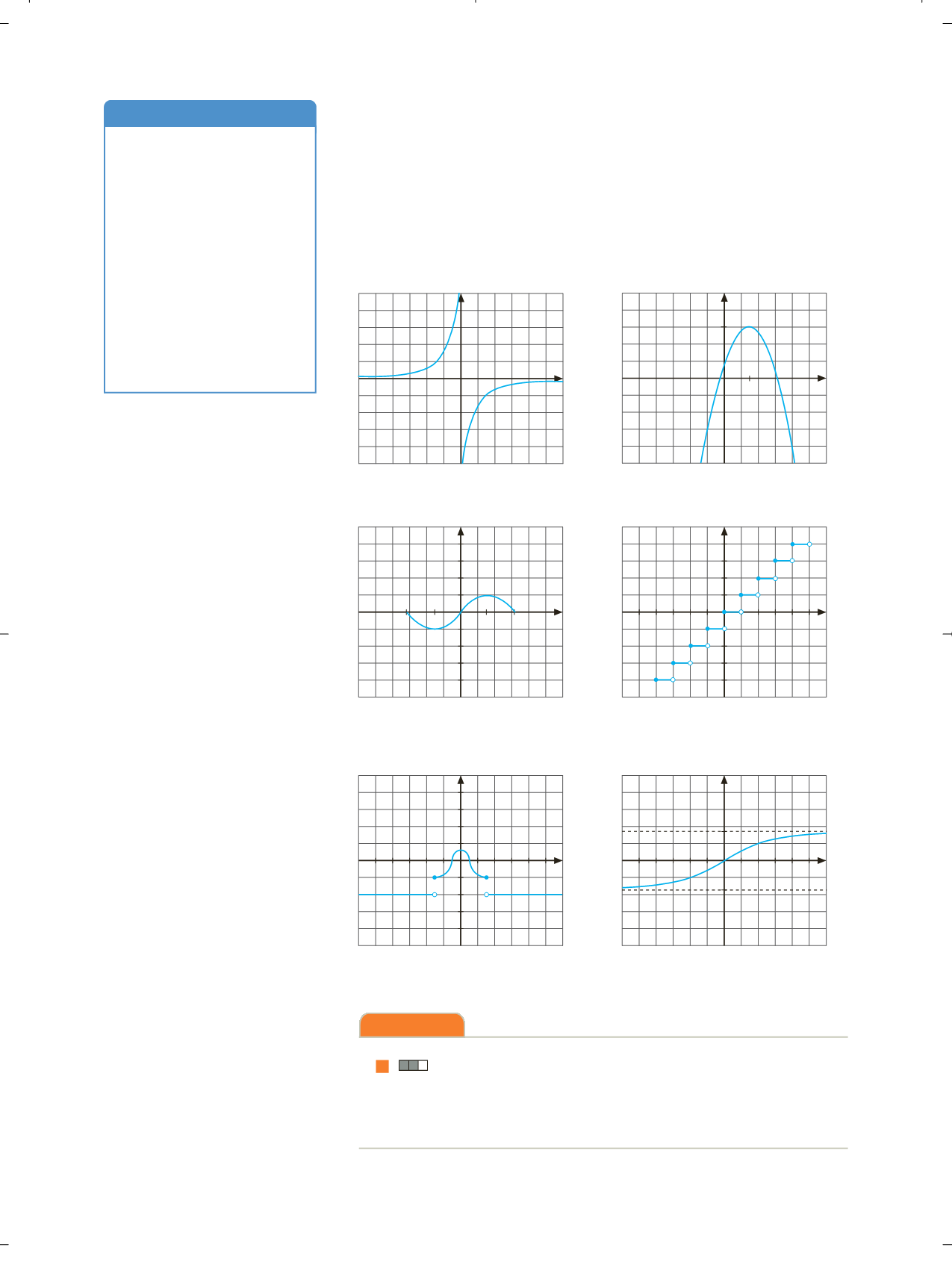
Para calcular el recorrido de funciones definidas gráficamente se determi-
na la
proyección
de la gráfica sobre el eje de ordenadas. Así el recorrido de
cada una de estas funciones es:
Rec
f
{0}
Rec
f
(
∞
,
f
(
a
)]
Rec
f
[ 1, 1]
Rec
f
Rec
f
{ 2}
1,
1
2
Rec
f
2
,
2
Calcula el recorrido de las siguientes funciones:
a)
f
(
x
)
x
2
1
c)
f
(
x
)
x
2
2
x
1
b)
f
(
x
)
x
2
x
d)
f
(
x
) 7
Solución:
a)
[ 1,
∞
)
b)
[ 1/4,
∞
)
c)
(
∞
, 0]
d)
{7}
7
Actividades
O
X
Y
O
X
Y
f(a)
a
F
IGURA
8.14.a.
F
IGURA
8.14.b.
1
2
3
4
O
X
π
/2
2
3
Y
4
π
π
/2
π
1
2
3
4
O
X
1 2 3 4 5
2 4
2
3
Y
4
F
IGURA
8.14.c.
F
IGURA
8.14.d.
1
2
3
4
O
X
1 2 3 4 5
2 4
2
3
Y
4
O
X
1 2 3 4 5
2 4
Y
y
π
/2
y
π
/2
F
IGURA
8.14.e.
F
IGURA
8.14.f.
OBSERVA
El recorrido de las
funciones poli-
nómicas de primer grado,
de la
forma
f
(
x
)
ax b,
es .
El recorrido de las
funciones poli-
nómicas de segundo grado,
de la
forma
f
(
x
)
ax
2
bx c,
es un
subconjunto de
que se deter-
mina a partir de la ordenada de
su vértice,
y
v
, y del signo del coefi-
ciente
a:
Si
a
0, entonces:
Rec
f
(
x
) [
y
v
,
∞
)
Si
a
0, entonces:
Rec
f
(
x
) (
∞
,
y
v
]


