214
5.2.
Monotonía
Se entiende por
monotonía
de una función su variación con respecto a
la variable independiente. Este concepto engloba los de crecimiento y decre-
cimiento:
Una función,
f
(
x
), es
creciente
en un intervalo (
a, b
) de su dominio si
para cualquier par de valores
x
1
y
x
2
del intervalo, con
x
2
x
1
, se cumple
que
f
(
x
2
)
f
(
x
1
). En caso de que se cumpla
f
(
x
2
)
f
(
x
1
), la función es
estrictamente creciente
en el intervalo (
a, b
). (figura 8.17.a)
Una función,
f
(
x
), es
decreciente
en un intervalo (
a, b
) de su dominio si
para cualquier par de valores
x
1
y
x
2
del intervalo, con
x
2
x
1
, se cumple
que
f
(
x
2
)
f
(
x
1
). En caso de que se cumpla
f
(
x
2
)
f
(
x
1
), la función es
estrictamente decreciente
en el intervalo (
a, b
). (figura 8.17.b)
F
IGURA
8.17.a.
F
IGURA
8.17.b.
Una función,
f
(
x
), presenta un
máximo
en un punto de un intervalo (
a, b
)
de su dominio si pasa de creciente a decreciente. Y presenta un
mínimo
se
pasa de decreciente a creciente.
Ejercicios resueltos
Indicar los intervalos de crecimiento y decrecimiento de f
(
x
)
x
2
x
2.
La función es decreciente en el intervalo (
∞
, 1/2) y creciente en el inter-
valo (1/2,
∞
). (figura 8.18)
En el punto
V
la función presenta un mínimo.
Indicar los intervalos de crecimiento y decrecimiento de f
(
x
)
2
x
2
3
x
.
La función es creciente en el intervalo (
∞
, 3/4) y decreciente en el inter-
valo (3/4,
∞
). (figura 8.19)
En el punto
V
la función presenta un máximo.
F
IGURA
8.18.
F
IGURA
8.19.
▼
▼
Y
X
a
b
Y
X
a
b
X
Y
3 2
1 2 3
2
3
4
1
3
2
1
4
O
f
(
x
)
x
2
x
2
V
1
2
,
9
4
X
Y
1
1
f
(
x
)
2
x
2
3
x
V
3
4
,
9
8
O
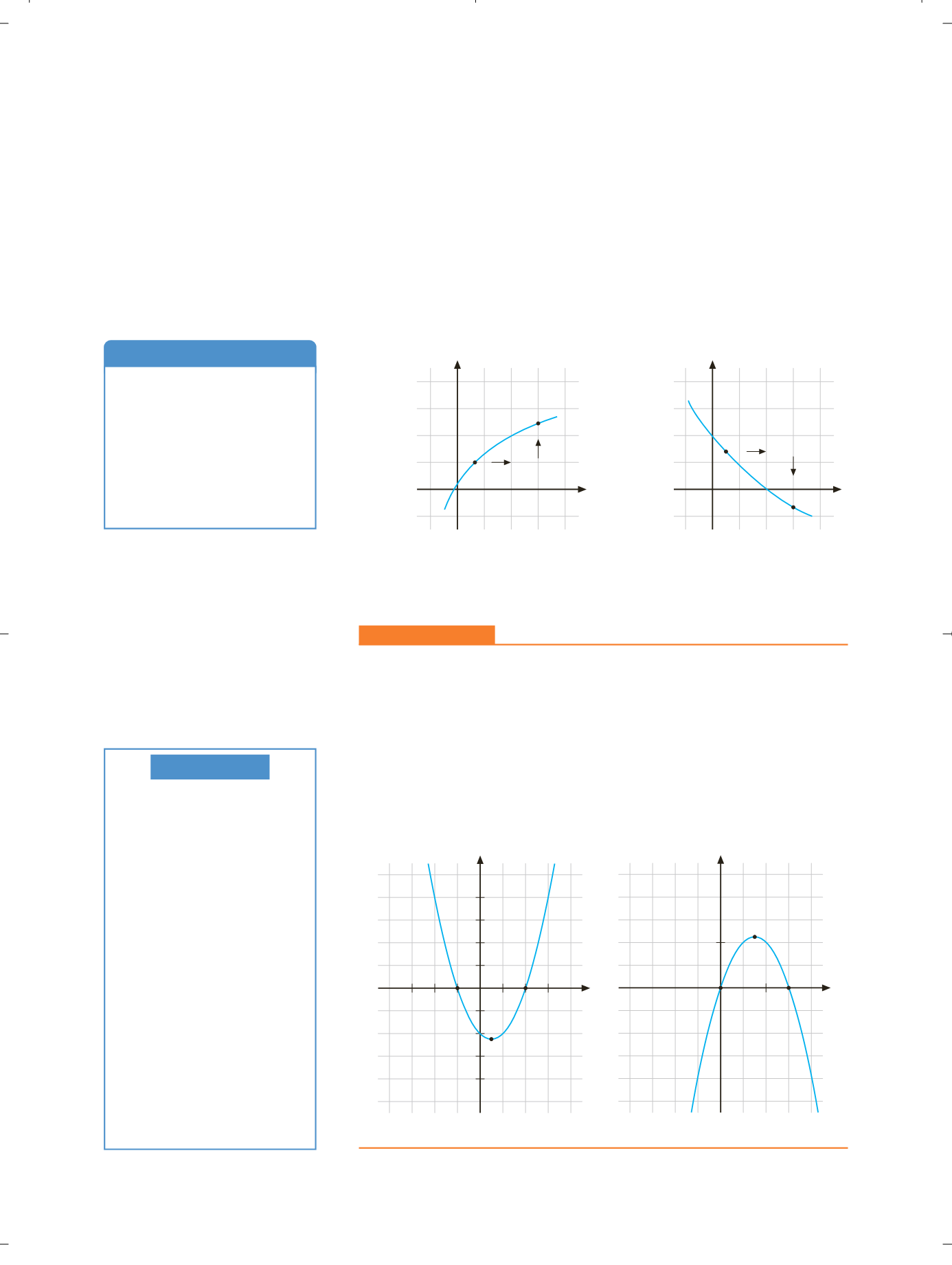
OBSERVA
Gráficamente, una función es cre-
ciente si al desplazar el valor de
las abscisas hacia la derecha, el
valor de las ordenadas sufre un
desplazamiento hacia arriba. Si,
por el contrario, la función es de-
creciente, el valor de las ordena-
das sufre un desplazamiento ha-
cia abajo.
RECUERDA
Si la pendiente de una recta es
positiva, la
función polinómica
de primer grado
que representa
es creciente. Si, por el contrario, la
pendiente es negativa, es decre-
ciente.
La representación gráfica de
una
función polinómica de se-
gundo grado
es una parábola.
Si el coeficiente del término de
segundo grado es positivo, la pa-
rábola tiene las ramas hacia arriba
y su vértice, deja a la izquierda el
intervalo de decrecimiento, y a su
derecha el de crecimiento.
Si el coeficiente del término de
segundo grado es negativo, la pa-
rábola tiene las ramas hacia aba-
jo y su vértice deja a la izquierda
el intervalo de crecimiento y a su
derecha el de decrecimiento.


