241
Movimientos en una y dos dimensiones
3.4.
Superposición de movimientos uniformes
¿Qué ocurre cuando cruzamos un río atravesando sus aguas?
Todos sabemos lo que significa ir a favor o en contra de la corriente. Vectorialmente
quiere decir que nuestra velocidad y la del curso del agua se suman (a favor de la
corriente) o se restan (a contracorriente).
Pero,
¿qué pasa cuando una barca cruza el río perpendicularmente, suponiendo que
su velocidad y la de la corriente son constantes?
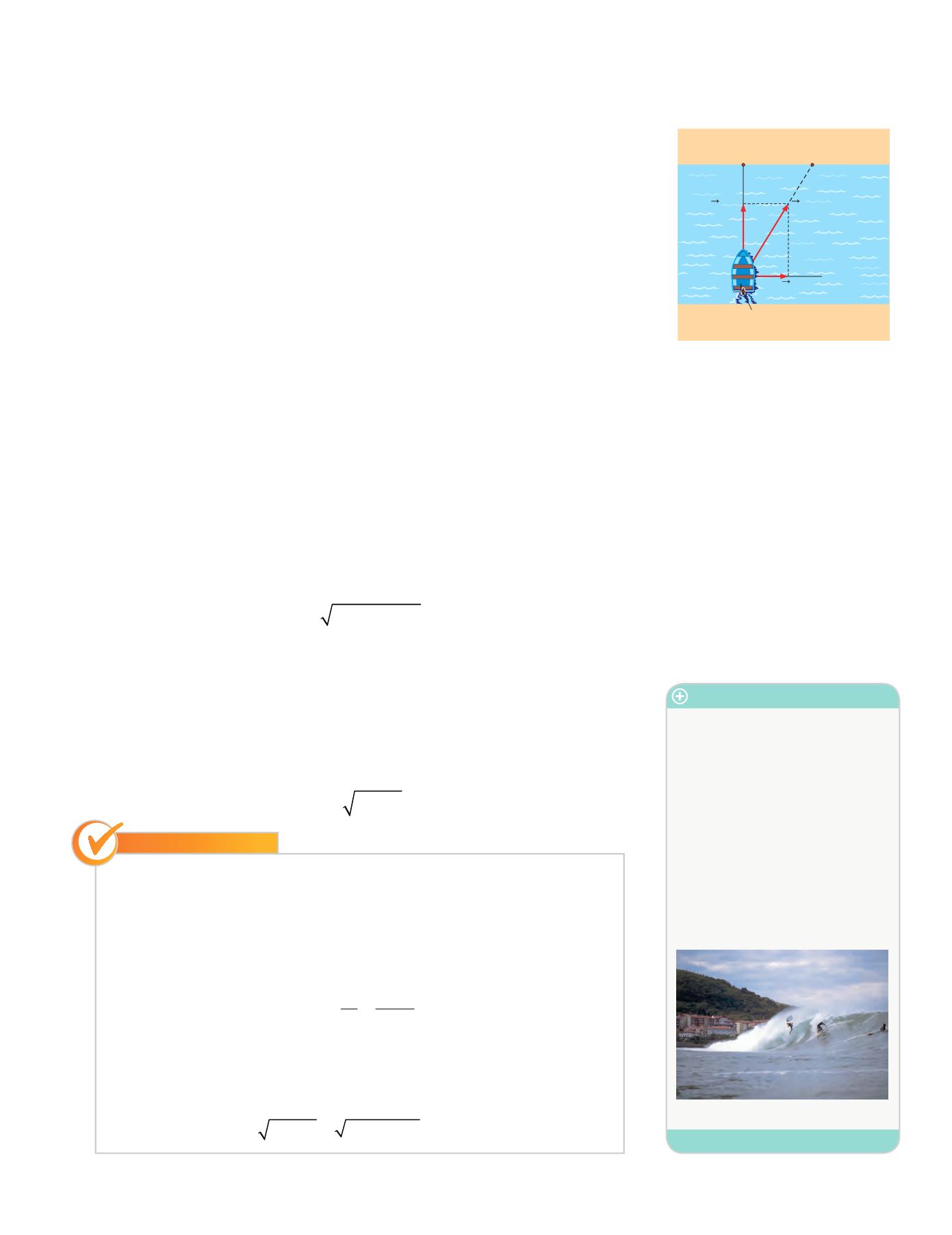
Este es un caso de composición de dos movimientos rectilíneos y uniformes (figura
10.27).
Imagina un eje de coordenadas donde
x
es la dirección de la corriente e
y
la del mo-
vimiento que seguiría la barca en ausencia de corriente. En caso de que no existiera
corriente, la barca cruzaría la anchura del río
∆
y
en un tiempo
t
determinado solo
por la velocidad de la barca
v
y
, según:
∆
y
=
v
y
t
Sin embargo, la velocidad de la corriente,
v
x
, hace que en ese mismo tiempo,
t
, la
barca sufra una «deriva» o desplazamiento
∆
x
en la dirección de dicha corriente,
dado por:
∆
x
=
v
x
t
De modo que el desplazamiento neto efectuado por la barca en ese tiempo es:
Δ
r
=
Δ
x
i
+
Δ
y
j
Por tanto, la distancia real que recorre será:
d
=
(
Δ
x
)
2
+
(
Δ
y
)
2
En consecuencia, la barca no cruza «perpendicularmente» el río, sino que su punto
de llegada se habrá desplazado en la dirección de la corriente.
Del mismo modo, la velocidad total de la barca es la superposición de la de su motor
o sus remos (
v
y
) y la de la corriente (
v
x
). Así pues:
v
=
v
x
i
+
v
y
j
Por tanto, el valor de la velocidad «real» de la barca (para un observador externo), será:
v
=
v
x
2
+
v
y
2
La ola izquierda de Mundaka
Los aficionados al surf sienten una es-
pecial predilección por esta ola, que
se forma con vientos del sur-sudoeste
y recorre la ría de Mundaka (Bizkaia),
en la Reserva de la Biosfera de Urdai-
bai. Para aprovechar al máximo la ola,
los surferos se desplazan lateralmente
con ella, añadiendo su propia veloci-
dad «transversal» (v
t
) a la velocidad
de avance de la ola (v
ola
), de modo que
la velocidad final es la composición de
ambas y el disfrute es máximo.
Figura 10.28.
Una lancha trata de cruzar perpendicularmente un río de 100 m de an-
cho moviéndose en esa dirección a una velocidad constante de 8 m/s. Si la
corriente del río lleva una velocidad de 12 m/s hacia la izquierda, ¿a qué
distancia del punto deseado se encontrará la embarcación al llegar a la otra
orilla? ¿Qué distancia habrá recorrido, en realidad, cruzando el río?
Si no hubiese corriente, el tiempo que tardaría en cruzar sería:
y
=
v
y
t
⇒
t
=
y
v
y
=
100 m
8 m/s
=
12,5 s
En ese tiempo, la lancha sufre un desplazamiento,
x
, en la dirección de la corriente:
x
=
v
corr
t
=
12 m/s
⋅
12,5 s
=
150 m
Llegará a 150 m del punto deseado, y el desplazamiento neto efectuado será:
Δ
r
=
x
2
+
y
2
=
100
2
+
150
2
=
180,27 m
EJERCICIO RESUELTO 3
Figura 10.27.
El movimiento final de la barca
es la superposición del movimiento de esta
y el del río.
punto
de salida
punto
de llegada
v
barca
v
resultante
v
rio


