242
Unidad 10
4.
Movimientos circulares
En la figura 10.29 puedes observar que los cuerpos A y B describen círculos de for-
ma acompasada, de modo que al cabo de cierto tiempo, ∆
t
, se encuentran en las
posiciones indicadas.
¿Se desplazan con la misma velocidad? ¿Qué tienen en común
ambos movimientos?
Seguramente habrás llegado a la conclusión de que sus velocidades «lineales» no
son iguales (el calificativo «lineal» se aplica aquí para distinguir esta velocidad,
v,
de
la velocidad «angular», que será definida más adelante). Sin embargo, lo que sí re-
sulta ser igual para ambos cuerpos es el ángulo descrito en función del tiempo. Ade-
más, cuanto más rápidamente se muevan con mayor rapidez describirán el ángulo.
4.1.
Las magnitudes cinemáticas angulares
El ejemplo anterior nos muestra la conveniencia de tratar los movimientos circula-
res en términos de magnitudes angulares, en lugar de las magnitudes cinemáticas
lineales empleadas hasta el momento. Las magnitudes circulares son la
posición
angular
(
θ
), la
velocidad angular
(
ω
) y la
aceleración angular
(
α
).
La posición angular
En la figura 10.29 los dos móviles, que se mueven acompasadamente, están siempre
en idéntica posición relativa uno respecto del otro. Diremos que su posición angular
es la misma.
Se define la
posición angular (
θ
)
como el
ángulo descrito por el vector de
posición
del móvil
expresado en radianes.
En consecuencia:
θ
=
s
r
Donde
s
es el arco de circunferencia recorrido por el móvil y
r
el radio de dicha
circunferencia (figura 10.30).
El vector de posición de un cuerpo que describe círculos se expresará en función de
la posición angular, según la expresión:
r
=
r
cos
θ
i
+
r
sen
θ
j
Siendo su módulo, como puedes comprobar en la figura 10.31, igual al radio.
La velocidad angular
Cuanto más rápidamente se desplaza el cuerpo, mayor es el ángulo descrito por
unidad de tiempo.
Se define la
velocidad angular (
ω
)
como la
rapidez con que se describe el
ángulo.
De ese modo, definida en términos de velocidad angular media:
ω
=
Δ
θ
Δ
t
La
unidad
de velocidad angular en el SI es el
radián por segundo (rad/s).
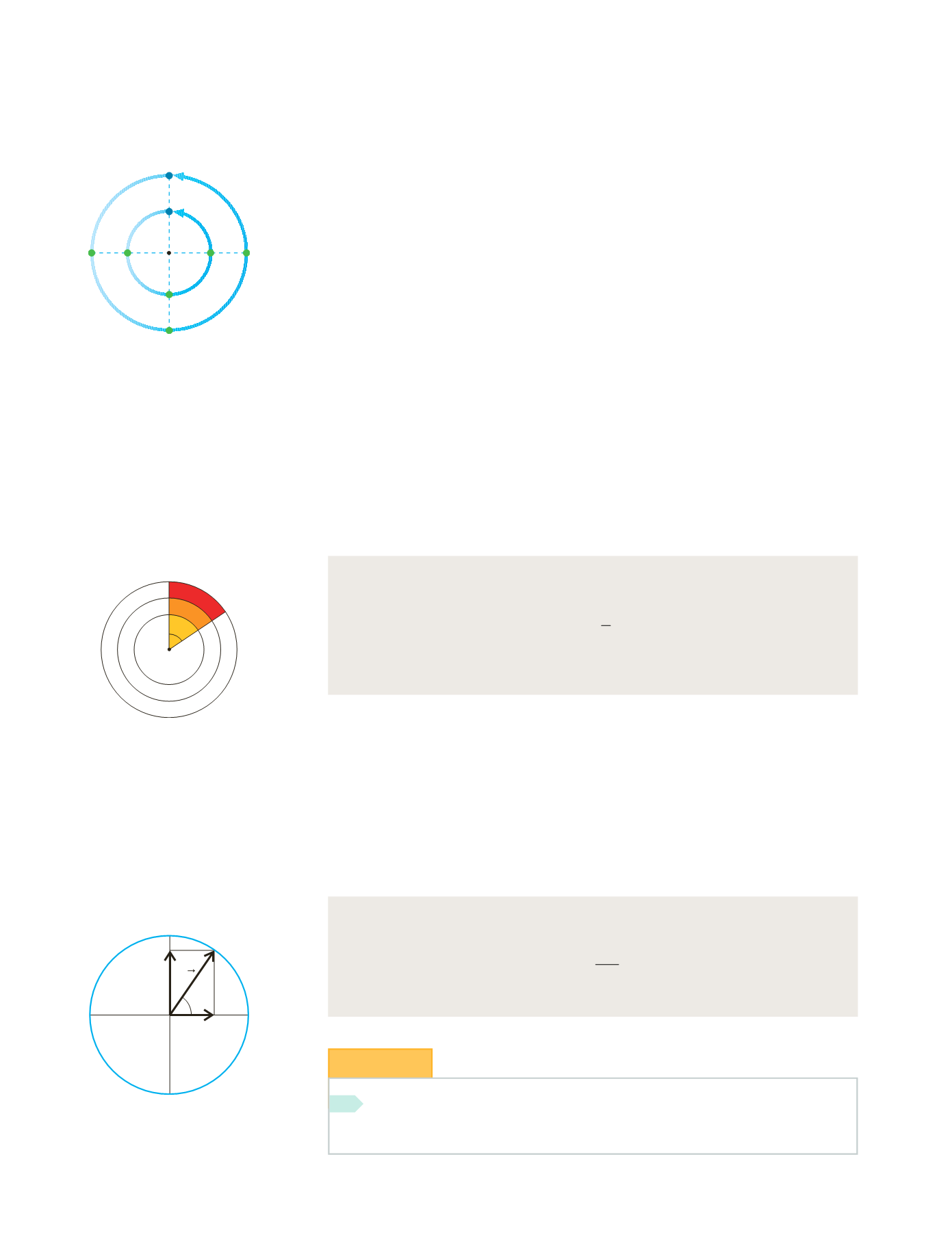
Figura 10.29.
Los puntos A y B efectúan
una vuelta completa en el mismo tiempo;
sin embargo, los espacios que recorren son
distintos, por lo que no se mueven con la
misma velocidad lineal.
A
B
Figura 10.31.
En un movimiento circular, el
modulo del vector de posición,
r
, coincide
con el radio de la circunferencia,
r,
que
describe.
θ
r
cos
θ
r
sen
θ
r
Figura 10.30.
Para un mismo ángulo, la
relación entre el arco de la circunferencia
s
y el radio
r
es constante e igual al valor del
ángulo en radianes.
r
1
r
2
r
3
θ
S
1
S
2
S
3
Actividades
19
Un cuerpo recorre 4 m cada segundo por la periferia de una pista circular
de 5 m de radio. ¿Cuál es su velocidad angular en rad/s? Escribe la expre-
sión de su vector de posición al cabo de 3 s.
Solución:
ω
=
0,8 rad/s


