216
5.4.
Simetrías
Una función,
f
(
x),
es
par
si se cumple que, para cualquier
x
Dom
f,
f
(
x
)
f
(
x
).
En este caso, la gráfica de la función es
simétrica respecto del eje de
ordenadas,
puesto que si existe el par (
x, f
(
x
)), también existe el par
(
x, f
(
x
)), y, por tanto, para cualquier punto (
x, y
) de la gráfica existe su simé-
trico (
x, y
) respecto del eje de ordenadas.
Ejercicios resueltos
Determinar si la función f
(
x
)
x
2
x
2
1
es par.
Es una función par, puesto que
f
(
x
)
f
(
x
).
Observa que la gráfica es simétrica respecto del eje de ordenadas:
F
IGURA
8.24.
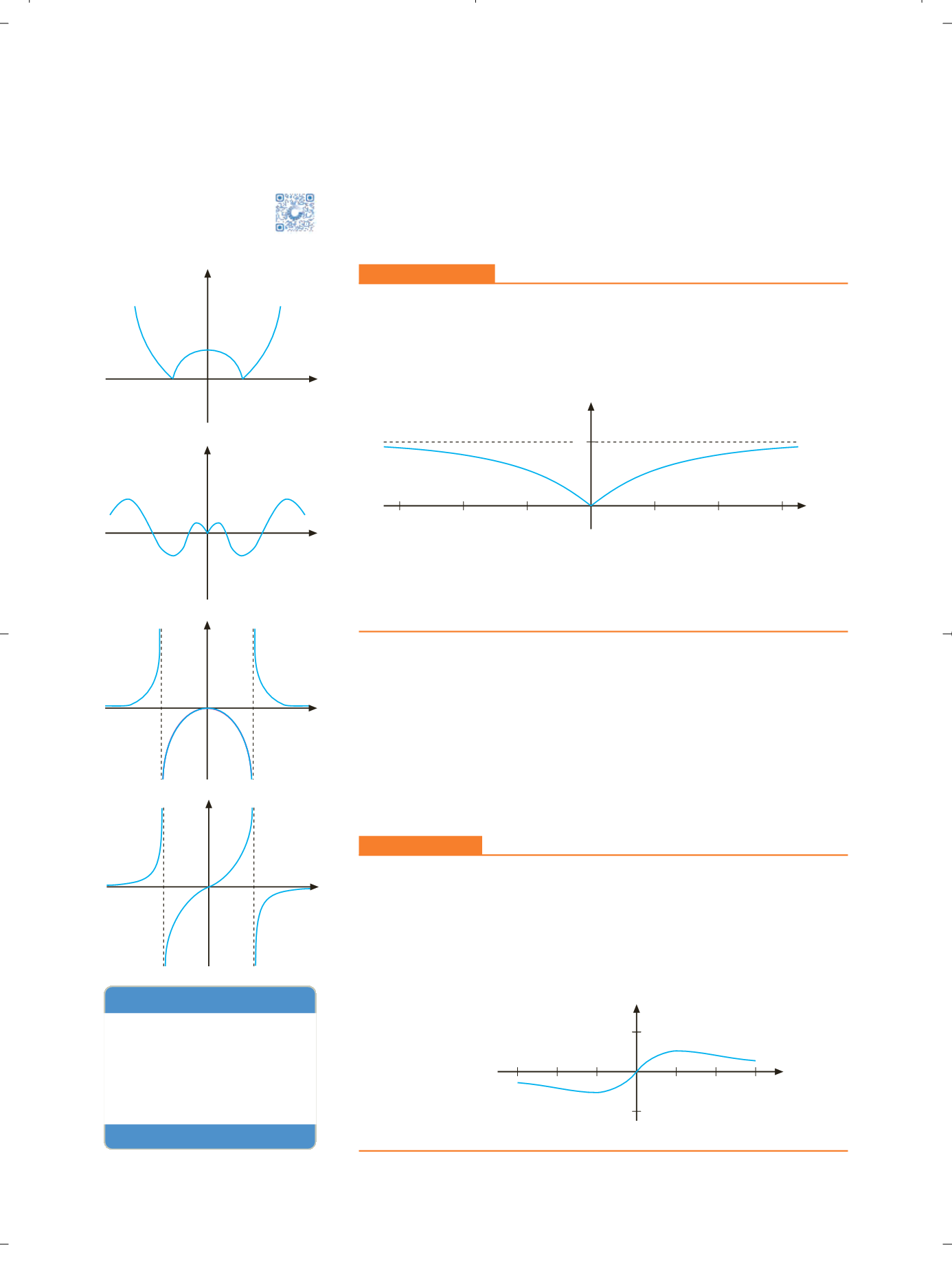
Determinar si son pares las funciones de las figuras del margen
.
Son pares las funciones correspondientes a las gráficas
a, b
y
c.
La función
correspondiente a la gráfica
d
no lo es.
Una función,
f
(
x
)
,
es
impar
si se cumple que, para cualquier
x
Dom
f,
f
(
x
)
f
(
x
).
En este caso, la gráfica de la función es
simétrica respecto del origen de
coordenadas
puesto que si existe el par (
x, f
(
x
)), existe (
x
,
f
(
x
)). Por tanto,
dado el punto (
x, y
) de la gráfica de la función, también existe el punto
(
x
,
y
), que es el resultado de realizar dos simetrías consecutivas respecto
de los ejes de coordenadas.
Así, la función correspondiente a la gráfica de la figura 8.25.d es impar.
Ejercicio resuelto
Determinar si la función f
(
x
)
x
2
x
1
es par o impar.
Es impar, puesto que
f
(
x
)
(
x
)
2
x
1
x
2
x
1
f
(
x
).
Observa la representación gráfica de
f
(
x
) en la figura 8.26. Es simétrica
respecto del origen de coordenadas.
F
IGURA
8.26.
▼
▼
x
2
x
2
1
(
x
)
2
(
x
)
2
1
▼
F
IGURA
8.25.a.
Y
X
1
1
1
2
2
O
O
X
Y
F
IGURA
8.25.b.
X
Y
O
F
IGURA
8.25.c.
X
Y
O
F
IGURA
8.25.d.
X
Y
O
X
Y
1
1
1
1
2
2
O
Simetría de funciones
Hay funciones que no presentan
sime-
tría
de ningún tipo. Otras, en cambio,
son simétricas respecto de rectas que
no son los ejes de coordenadas.
Para el estudio general de funciones, las
simetrías son muy útiles.
ma1b900


