105
Estructura atómica y molecular
ESTRATEGIAS DE RESOLUCIÓN
4
Por tanto,
λ
=
1
97 491,2 cm
−
1
=
1,03
⋅
10
−
5
cm
υ
=
3
⋅
10
10
cm s
−
1
1,03
⋅
10
−
5
cm
=
2,92
⋅
10
15
s
−
1
❚❚
La última línea:
1
λ
=
109 677,6 cm
−
1
⋅
1
1
2
−
1
∞
⎛
⎝
⎜⎜⎜
⎞
⎠
⎟⎟⎟⎟
=
=
109 677,6 cm
−
1
⋅
1
−
0
(
)
=
109 677,6 cm
−
1
Por tanto,
λ
=
1
109 677,6 cm
−
1
=
9,12
⋅
10
−
6
cm
υ
=
3
⋅
10
10
cm s
−
1
9,12
⋅
10
−
6
cm
=
3,29
⋅
10
15
s
−
1
5
Calcula la longitud de onda, la frecuencia, el núme-
ro de onda y la energía de la radiación emitida por un
electrón situado en el nivel
n
=
4 al caer al
n
=
2. ¿A qué
serie pertenece esa raya?
Estrategia de resolución
Para calcular la longitud de onda aplicamos la ecuación de
Rydberg:
1
λ
=
R
1
n
1
2
−
1
n
2
2
⎛
⎝
⎜⎜⎜⎜
⎞
⎠
⎟⎟⎟⎟⎟
Si sustituimos,
n
2
=
4 y
n
1
=
2, obtenemos el número de onda:
υ
=
1/
λ
=
2055000 m
−
1
; por tanto,
λ
=
4,87
⋅
10
−
7
m
Para calcular la frecuencia empleamos esta expresión:
υ
=
c
λ
=
3
⋅
10
8
m/s
4,87
⋅
10
−
7
m
=
6,16
⋅
10
14
s
−
1
Ahora ya es posible calcular la energía de la radiación emitida
recurriendo a la ecuación de Planck:
E
=
h
υ
=
6,63
⋅
10
−
34
J s
⋅
6,16
⋅
10
14
s
−
1
=
4,08
⋅
10
−
19
J
Como el nivel al que ha saltado el electrón es el 2, la raya
pertenece a la serie de Balmer.
6
Calcula la energía cinética del electrón emitido por
el átomo de cesio al iluminarlo con una radiación de
λ
=
600 nm. Datos:
h
=
6,63
⋅
10
−
34
Js;
c
=
3
⋅
10
8
m
⋅
s
−
1
;
W
extracción del Cs
=
2 eV; 1 eV
=
1,6
⋅
10
−
19
J
Estrategia de resolución
Transformamos 2 eV a julios y 600 nm a m:
2 eV
⋅
1,6
⋅
10
−
19
J/eV
=
3,2
⋅
10
−
19
J; 600 nm
=
6
⋅
10
−
7
m
Calculamos la frecuencia de la luz incidente:
υ
=
c
λ
=
3
⋅
10
8
m s
−
1
6
⋅
10
−
7
m
=
5
⋅
10
14
s
−
1
Aplicamos la ecuación del efecto fotoeléctrico y sustituimos:
h
υ
=
W
extracción
+
E
c
6,63
⋅
10
−
34
J s
⋅
5
⋅
10
14
s
−
1
=
3,2
⋅
10
−
19
J
+
E
c
E
c
=
0,1
⋅
10
−
19
J
=
0,1
⋅
10
−
19
J/1,6
⋅
10
−
19
J/eV
=
0,06 eV
Técnicas espectroscópicas
7
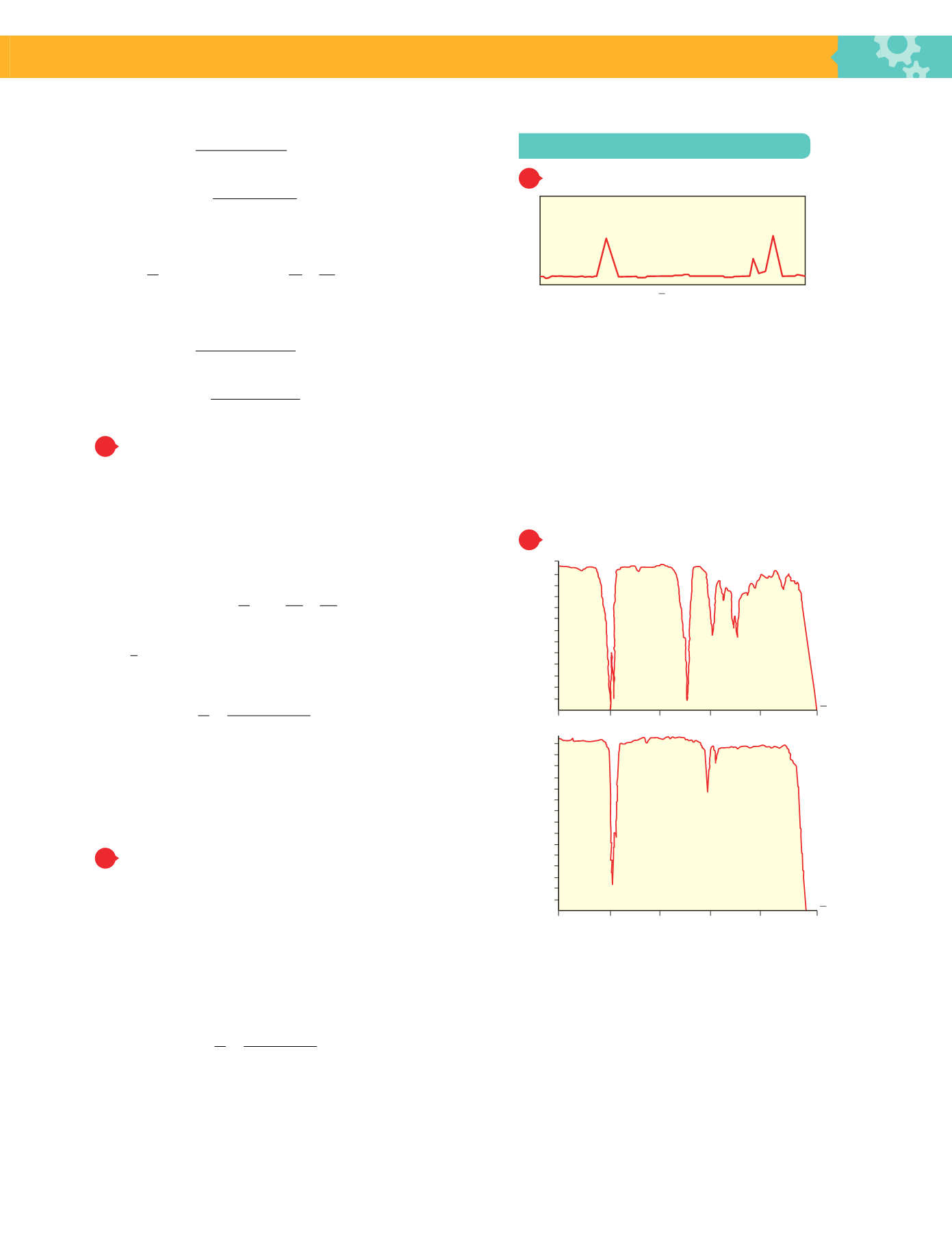
Observa este espectro y di si la muestra es agua.
ν
(cm
−
1
)
1600
4000
600
6
Estrategia de resolución
Analizando el espectrograma de izquierda a derecha, observa-
mos 3 picos. El primero aparece a un número de onda cercano
a los 1600 cm
−
1
(el de flexión del H
2
O aparece a 1595 cm
−
1
)
y los otros dos en las proximidades de 4000 cm
−
1
(el de ten-
sión simétrica del H
2
O aparece a 3652 cm
−
1
y el de tensión
asimétrica a 3756 cm
−
1
). Por otra parte, de los dos picos de
la derecha, el más elevado es el segundo, lo que estaría de
acuerdo con la vibración de tensión asimétrica del agua, que
modifica el momento dipolar de la molécula en mayor cuantía
que el de tensión simétrica. Por lo tanto, la sustancia es agua.
8
Observa estos dos espectros de IR y saca conclusiones.
5
10
15
20
25
30
35
40
45
50
55
60
65
4000
3000
2000
1500
1000
450
ν
(cm
−
1
)
%T
5
10
15
20
25
30
35
40
45
50
55
60
65
4000
3000
2000
1500
1000
450
75
ν
(cm
−
1
)
70
%T
Estrategia de resolución
Al no ser exactamente iguales, es que pertenecen a mues-
tras distintas. No obstante, en ambos espectros, algunos pi-
cos aparecen al mismo número de onda: el que está cerca de
3000 cm
−
1
, puede corresponder a vibraciones de tensión de
enlaces C–H (tabla 4.5) y el que aparece hacia los 1500 cm
−
1
,
correspondería a vibraciones de flexión, también de enlaces
C–H. Por tanto, podríamos asegurar que ambas muestras
contienen algún tipo de hidrocarburo, si bien en la primera
este se encuentra mezclado con otro tipo de moléculas (llevan
el grupo carbonilo C
=
O, pues este grupo siempre aparece en
la región de 1660 a 1900 cm
−
1
).


