229
Movimientos en una y dos dimensiones
tiempo
t
posición
x
x
=
x
0
+
v
t
x
=
x
0
−
v
t
x
0
Figura 10.5.
Gráficas posición-tiempo de un
MRU para un cuerpo que se aleja (en negro)
y otro que se acerca (en rojo). En ambos
casos, la pendiente representa la velocidad.
Criterio de signos
En la ecuación anterior, al adjudicar un signo positivo a la velocidad la posición
x
en
cualquier instante será siempre superior a la posición inicial
x
0
. Es decir, el cuerpo
se alejará
del observador. Por el contrario, cabe la posibilidad de que el cuerpo
se
acerque
a este, de modo que
x
será, en ese caso, siempre menor que
x
0
, lo que im-
plica adjudicar el signo negativo a la velocidad, como puede verse en la figura 10.4.
La
ecuación de posición
del movimiento rectilíneo uniforme se generaliza así:
x
=
x
0
±
v t
❚❚
Signo positivo:
si el cuerpo se aleja del observador.
❚❚
Signo negativo:
si el cuerpo se acerca al observador.
Observa que, si representamos gráficamente la posición frente al tiempo en un
MRU, se obtiene una recta cuya ordenada en el origen es
x
0
y cuya pendiente es el
valor de la velocidad
v.
La pendiente es positiva si el cuerpo se aleja de observador y
negativa si se acerca, como se aprecia en la figura 10.5.
Por otro lado, si representamos la velocidad de este movimiento frente al tiempo
obtendremos una recta horizontal, como corresponde al hecho de que la velocidad
sea constante (figura 10.6). El interés de esta representación radica en que el área
del rectángulo encerrado bajo la gráfica es igual a
v
∆
t
(altura
⋅
base) y corresponde
al desplazamiento efectuado
∆
x
que equivale, en este caso, al espacio recorrido.
Figura 10.6.
El área encerrada bajo la gráfica
v-t
representa el desplazamiento efectuado
o espacio recorrido.
t
v
velocidad
velocidad constante
desplazamiento
efectuado
tiempo
Actividades
2
¿Cuánto tarda la luz del sol
en llegar a la Tierra, teniendo
en cuenta que el Sol se halla a
una distancia media de la Tierra
de 149600000 km y que la luz
se propaga aproximadamente a
3
⋅
10
8
m/s? (Resuelve la actividad
situándote tú mismo como ori-
gen del sistema de referencia.)
Solución:
Aproximadamente 8 min
3
Las ecuaciones de movi-
miento de dos vehículos, A y B,
son
x
A
=
5
t
m y
x
B
=
140
−
2
t
m.
Determina:
a)
¿Qué distancia los separa ini-
cialmente?
b)
¿En qué sentidos relativos
se mueven uno respecto del
otro?
c)
¿En qué instante se cruzan?
d)
Representa el movimiento de
ambos vehículos en una mis-
ma gráfica
x-t.
Solución:
a)
140 m;
c)
20 s
4
Dos vehículos (A y B) parten
uno al encuentro de otro desde
dos localidades que distan entre
sí 400 km. El vehículo A viaja a
100 km/h, mientras que el B, que
se pone en marcha un cuarto
de hora después, lo hace a 120
km/h.
a)
¿Cuánto tiempo pasa desde
que parte A hasta que se pro-
duce el encuentro?
b)
¿Qué distancia ha recorrido
el vehículo A?
c)
Representa el movimiento de
ambos vehículos en una mis-
ma gráfica
x-t
.
Solución:
a)
117 min 6 s;
b)
195 km
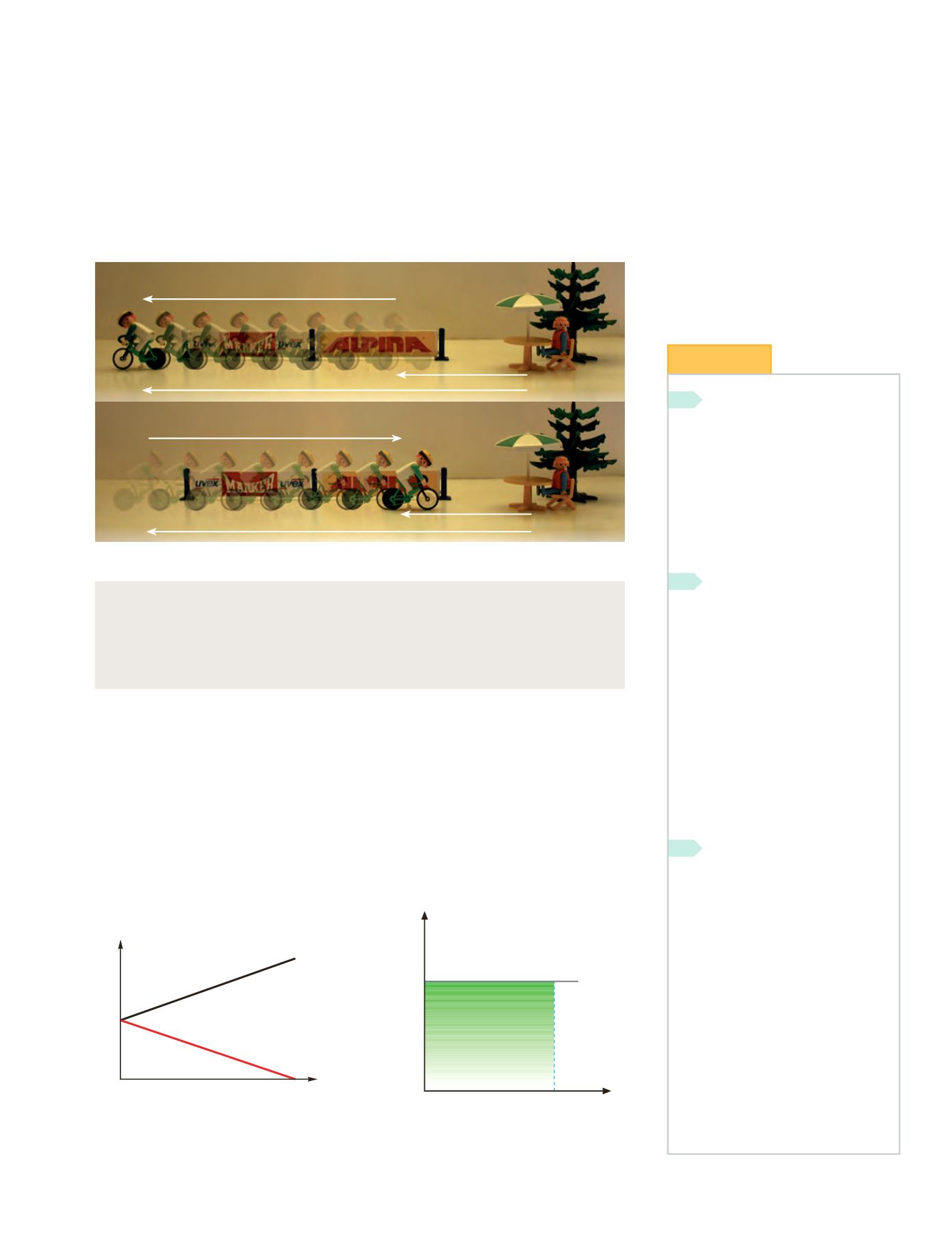
Figura 10.4.
La velocidad es positiva si el cuerpo se aleja del observador y negativa si se acerca a este.
x
0
+
vt
x
Observador
x
−
vt
x
0
Observador


