239
Movimientos en una y dos dimensiones
3.3.
Movimiento parabólico completo
¿Qué hace un saltador de longitud para lograr una marca?
Primero inicia una carrera
horizontal para tratar de alcanzar velocidad, y en el momento del salto se impulsa
oblicuamente sobre el suelo. Así consigue despegar con una velocidad inicial,
v
0
,
que forma cierto ángulo con el suelo. Esta velocidad inicial tiene dos componentes:
v
0
x
=
v
0
cos
α
v
0
y
=
v
0
sen
α
Dichas componentes producen el avance (
v
0
x
) y la elevación (
v
0
y
) necesarios durante
el salto. La componente horizontal de la velocidad no está afectada por la actuación
vertical de
g,
por lo que permanece constante durante todo el movimiento. Sin em-
bargo, la componente vertical sí lo está, exactamente igual que si de un lanzamiento
vertical hacia arriba se tratara.
Por tanto, y habida cuenta de que este movimiento puede abordarse como la com-
posición de un MRU y un lanzamiento vertical hacia arriba, las únicas ecuaciones
que se precisan para describirlo son las de los movimientos componentes. Así, la
posición del saltador en el aire vendrá dada por:
❚❚
Componente horizontal de avance (MRU):
x
=
v
0
x
t
❚❚
Componente vertical de caída (MRUA):
y
=
y
0
( )
+
v
0
y
t
−
1
2
gt
2
❚❚
Ecuación de posición:
r
=
v
0
x
t
i
+
y
0
( )
+
v
0
y
t
−
1
2
gt
2
⎛
⎝
⎜⎜⎜⎜
⎞
⎠
⎟⎟⎟⎟
j
Debemos tener presente que un movimiento parabólico puede comenzar desde una
altura inicial (por ejemplo, saltos de trampolín de esquí). En ese caso, en la ecuación de
altura habría que contemplar la altura inicial
y
0
. Por eso, se ha escrito entre paréntesis.
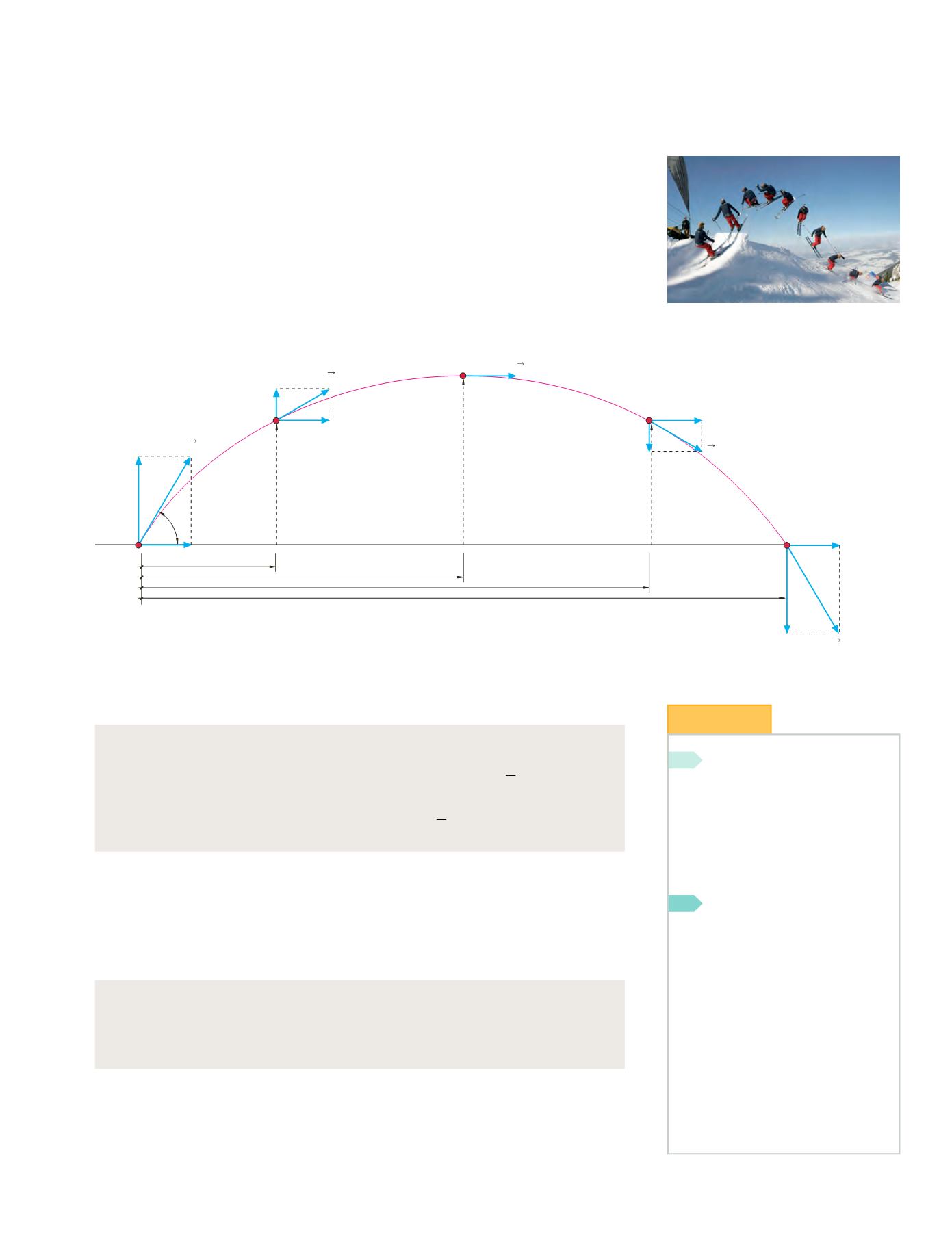
A su vez, la velocidad del saltador en el aire tendrá también dos componentes (una
de avance y otra de ascenso-descenso), como se aprecia en la figura 10.25.
❚❚
Velocidad de avance horizontal:
v
x
=
v
0
x
❚❚
Velocidad de caída vertical:
v
y
=
v
0
y
−
gt
❚❚
Ecuación de velocidad:
v
=
v
0
x
i
+
v
0
y
−
gt
(
)
j
Dos puntos característicos de un movimiento parabólico son el
alcance máximo
(la
marca de un saltador de longitud) y la
altura máxima
(la marca de un saltador de
altura, por ejemplo). Para determinar dichos parámetros y analizar de qué factores
dependen, solo debemos fijarnos en las características que definen a dichos puntos.
Actividades
13
Deduce la ecuación de la tra-
yectoria del saltador de longitud
que relaciona
x
con
y
. Comprue-
ba que se trata de la ecuación de
una parábola y emplea el mismo
procedimiento que se desarrolló
en la aplicación del lanzamiento
horizontal.
14
A partir de la ecuación de
la altura en el movimiento pa-
rabólico, despeja el tiempo
t
y
trata de analizar a continuación
el significado que encierra la ex-
presión obtenida. Por ejemplo:
a)
¿Qué significado tiene el do-
ble signo que se obtiene?
b)
¿Cuándo es única la solución
del tiempo? ¿Qué valor tiene?
c)
¿A qué punto corresponde
dicha solución única del tiem-
po? ¿Cuánto vale la altura en
ese punto?
Figura 10.25.
Secuencia fotográfica que
ilustra la trayectoria parabólica de un salto
de
freestyle
en esquí.
α
v
0
v
1
v
2
v
4
v
3
v
x
=
v
0
x
v
0
x
v
0
y
v
x
=
v
0
x
v
y
v
x
=
v
0
x
v
y
v
x
=
v
0
x
v
y
=
–
v
0
y
v
0
x
=
v
0
cos
α
v
0
y
=
v
0
sen
α
x
1
x
2
x
3
y
3
y
max
y
1
x
max
Figura 10.24.
Movimiento parabólico. La velocidad varía en distintos puntos de la trayectoria.


