220
6.3.
División de funciones
Sean las funciones
f
(
x
) y
g
(
x
); la función cociente, (
f/g
)(
x
), es el cociente
de las imágenes de
x
por
f
y por
g.
Si alguna de estas imágenes no está definida
para algún valor real, el cociente tampoco lo está. Así mismo, para los valores
del dominio de
g
en los que
g
(
x
) 0, la función cociente no está definida.
(
f
/
g
)(
x
)
f
(
x
)/
g
(
x
), donde Dom (
f
/
g
) {Dom
f
Dom
g
} {
x
Dom
g
⏐
(
g
)(
x
) 0}
Ejercicio resuelto
Dividir las funciones f
(
x
)
2
x
y
g
(
x
)
1
x
.
Sus respectivos dominios son Dom
f
(
∞
, 2] y Dom (
g
)
{0}.
La función (
f/g
)(
x
) será:
(
f/g
)(
x
)
1
2
/
x
x
x
2
x
Su dominio es: Dom (
f/g
) (
∞
, 2] {0} (
∞
, 0) (0, 2].
Si no se indica el dominio, la función (
f/g
)(
x
) debe escribirse como:
(
f/g
)(
x
)
1
2
/
x
x
6.4.
Composición de funciones
Dadas dos funciones,
f
(
x
) y
g
(
x
), la función (
g f
)(
x
), que se obtiene apli-
cando
g
a la imagen por
f
de
x, f
(
x
), se denomina
función compuesta de
f
y
g
.
f
g
x f
(
x
)
g
[
f
(
x
)] (
g f
)(
x
)
Análogamente, la función compuesta de
g
y
f
, (
f g
)(
x
), se obtiene apli-
cando
f
a la imagen por
g
de
x, g
(
x
):
g
f
x g
(
x
)
f
[
g
(
x
)] (
f g
)(
x
)
Observa que, aunque se aplique primero la función
f
(
x
) y después la
función
g
(
x
),
f
compuesta de
g
se escribe de derecha a izquierda:
(
g f
)(
x
)
Si el recorrido de la primera función que se aplica,
f
(
x
), está incluido en el
dominio de la segunda,
g
(
x
), el dominio de la composición de
f
(
x
) y
g
(
x
) es
el dominio de
f
(
x
).
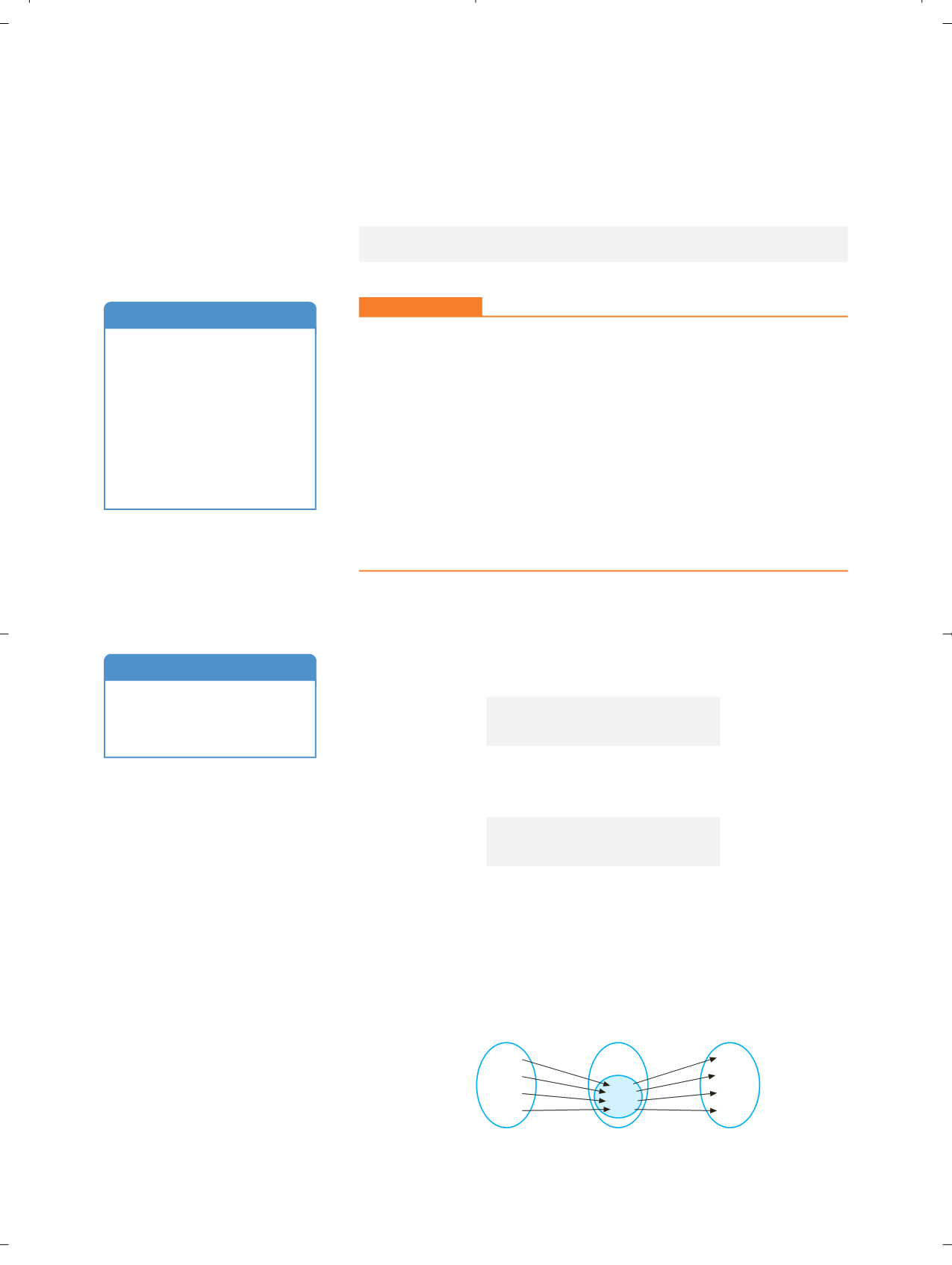
F
IGURA
8.32.
▼
f
g
Rec
g
Dom
g
Rec
f
Dom
f
OBSERVA
No se debe
simplificar
una opera-
ción con funciones si no se indica
su dominio; de lo contrario, el do-
minio que se deduce después de
la simplificación no es el correcto,
y la función no es la misma.
Para que dos funciones sean igua-
les, es indispensable que las imá-
genes sean iguales y que estén
definidas en el mismo dominio.
OBSERVA
En adelante, se escribirá
f g
y
g f
en lugar de (
f g
)(
x
) y (
g f
)(
x
), res-
pectivamente, para simplificar la
notación.


