222
7.
Función inversa respecto
de la composición de funciones
Antes de abordar el concepto de función inversa respecto de la compo-
sición, hay que definir los de función inyectiva, suprayectiva y biyectiva:
Una función es
inyectiva,
si y solo si,
f
(
a
)
f
(
b
)
⇒
a b;
en otras pala-
bras,
no hay
dos elementos del dominio con la misma imagen.
Así, por ejemplo,
f
(
x
)
1
3
2
x
es inyectiva, puesto que, si
f
(
a
)
f
(
b
), se
tiene que:
1
3
2
a
1
3
2
b
⇒
1 2
a
1 2
b
⇒
2
a
2
b
⇒
a b
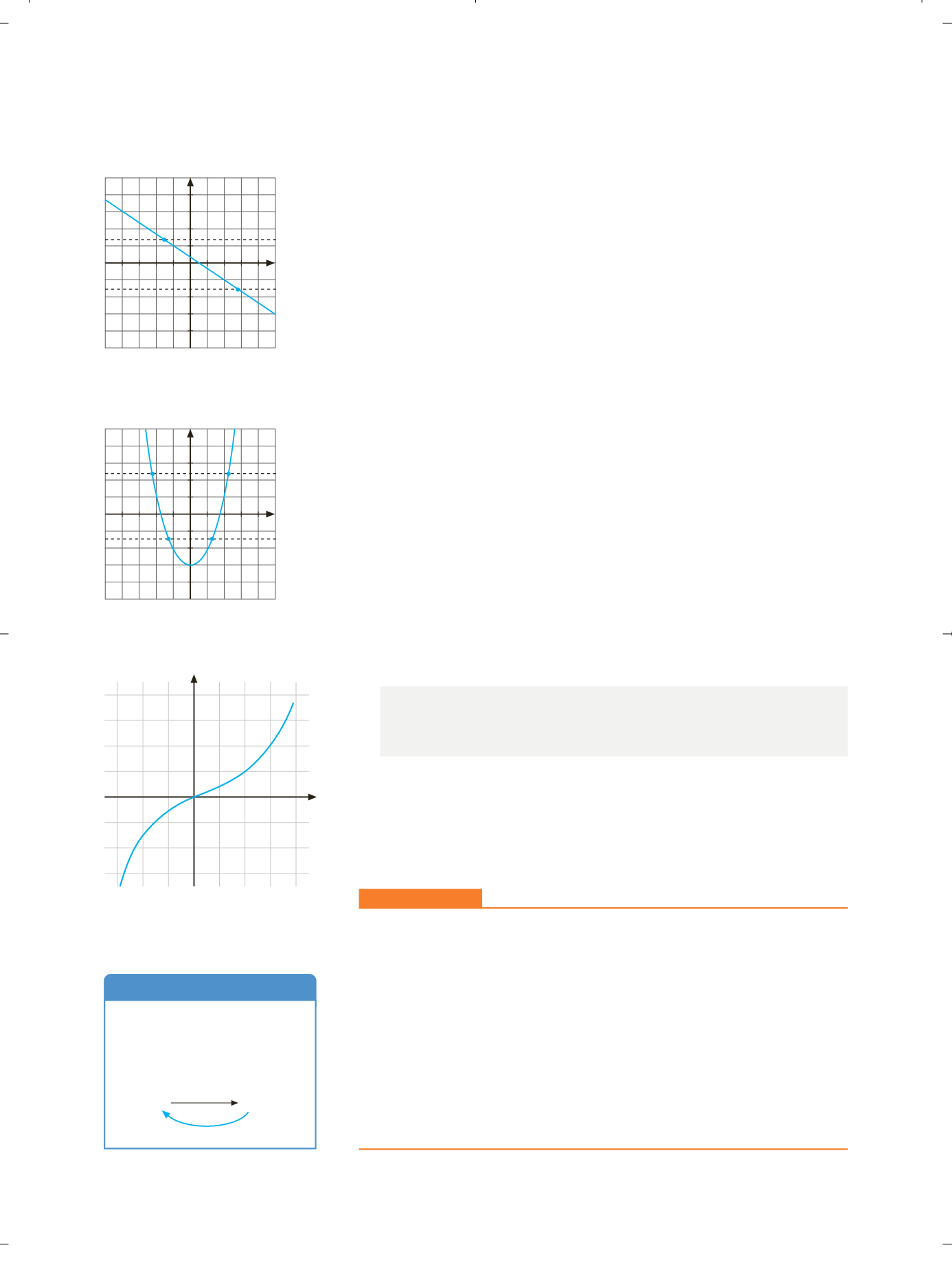
Gráficamente, una función es inyectiva si al trazar cualquier recta paralela
al eje de abscisas que corta a la gráfica, lo hace solo en un punto de esta
(figura 8.33).
Por ejemplo,
f
(
x
)
x
2
3 no es inyectiva (figura 8.34). De
a
2
3
b
2
3
se deduce que
a
2
b
2
, y esto significa que:
a
b
2
⇒
a b
Una función es
suprayectiva
o
exhaustiva,
si y solo si, su recorrido son
todos los números reales.
Así,
f
(
x
)
x
es una función suprayectiva, puesto que Rec
f
.
Por su parte,
f
(
x
)
no es suprayectiva, ya que Rec
f
{0}.
Una función es
biyectiva,
si y solo si, es inyectiva y suprayectiva al mismo
tiempo.
Dada una función inyectiva,
f
(
x
), se denomina
función inversa,
f
1
(
x
), a aquella
que cumple lo siguiente:
(
f f
1
)(
x
) (
f
1
f
)(
x
)
x
Para que una función tenga inversa respecto de la composición, es impres-
cindible que sea inyectiva. Si no es así, una misma imagen,
f
(
x
), puede tener
más de un original, por lo que la correspondencia inversa no sería una función:
a un valor
f
(
x
) le correspondería más de un valor,
f
1
[
f
(
x
)].
La composición de una función,
f
(
x
), y su inversa,
f
1
(
x
), es
conmutativa.
Ejercicio resuelto
Dada la función f
(
x
) 2
x
3,
que es biyectiva, ¿cuál es su inversa?
Su inversa será aquella función tal que
f
1
[
f
(
x
)]
x.
Por tanto, la imagen por
f
1
de
y f
(
x
) se obtiene sumando 3 a
y
y divi-
diendo el resultado de esta operación entre 2. Es decir:
f
1
(
y
)
y
2
3
Fíjate en que, si ahora se sustituye
y
2
x
3 en la expresión anterior,
tenemos que:
f
1
(
y
)
y
2
3 2
x
2
3 3
x,
es decir,
f
1
[
f
(
x
)]
x
▼
1
x
3
4
F
IGURA
8.33.
F
IGURA
8.34.
F
IGURA
8.35.
1
2
3
4
O
X
1 2 3 4
2 4
2
3
Y
4
Y
X
O
f
(
x
)
f
(
x
) es inyectiva,
y suprayectiva y,
por tanto, biyectiva
1
2
3
4
O
X
1 2 3 4
2 4
2
3
Y
4
OBSERVA
La
función inversa
o
recíproca
de
f
es aquella que
invierte
(
x, f
(
x
)), es
decir, a la imagen de
x
por
f, f
(
x
), le
hace corresponder de nuevo
x.
f
x
f
(
x
)
f
1


