14
Análisis
c)
Dom
f
, Rec
f
[0,
∞
)
La función
f
(
x
)
x E
(
x
) es la función que a cada número
real
x
, comprendido en un intervalo [
z, z
1), le hace co-
rresponder
x
z.
Por ejemplo,
f
(3,25)
3,25
3
0,25,
f
( 3,25) 0,75,
f
(0,5) 0,5 0 0,5,
f
( 0,5)
0,5 1 0,5.
Haz una tabla de valores y realiza su representación grá-
fica.
Características de las funciones
Dada la función
f
(
x
)
, determina sus intervalos de
signo constante.
Dom
f
{ 1} y
f
(
x
) 0 en
x
0, por lo tanto, intervalos
de signo constante son:
(
∞
, 1), ( 1, 0) y (0,
∞
)
f
( 2)
4
1
0
⇒
x
(
∞
,
1),
f
(
x
) 0
f
2
1 0
0
,2
,5
5
0
⇒
x
( 1, 0),
f
(
x
) 0
f
(1)
1
2
0
⇒
x
(0,
∞
),
f
(
x
) 0
Dada la función
f
(
x
)
, determina sus intervalos
de signo constante.
Dom
f
{0} y
f
(
x
) 0 en
x
2 y en
x
2, por lo tanto,
los intervalos de signo constante son los siguientes:
(
∞
, 2), ( 2, 0), (0, 2) y (2,
∞
)
f
( 3)
5
3
0
⇒
x
(
∞
,
2),
f
(
x
) 0
f
( 1)
3
1
0
⇒
x
( 2, 0),
f
(
x
) 0
f
(1)
1
3
0
⇒
x
(0, 2),
f
(
x
) 0
f
(3)
5
3
0
⇒
x
(2,
∞
),
f
(
x
) 0
x
2
4
x
32
x
2
x
1
31
X
O
Y
1
1
f
(
x
)
x
E
(
x
)
30
X
O
Y
1
2
1
1 2 3 4
2 1
3 45 6
5 6
3
4
5
3
2
4
5
y
=
x
2
2
x
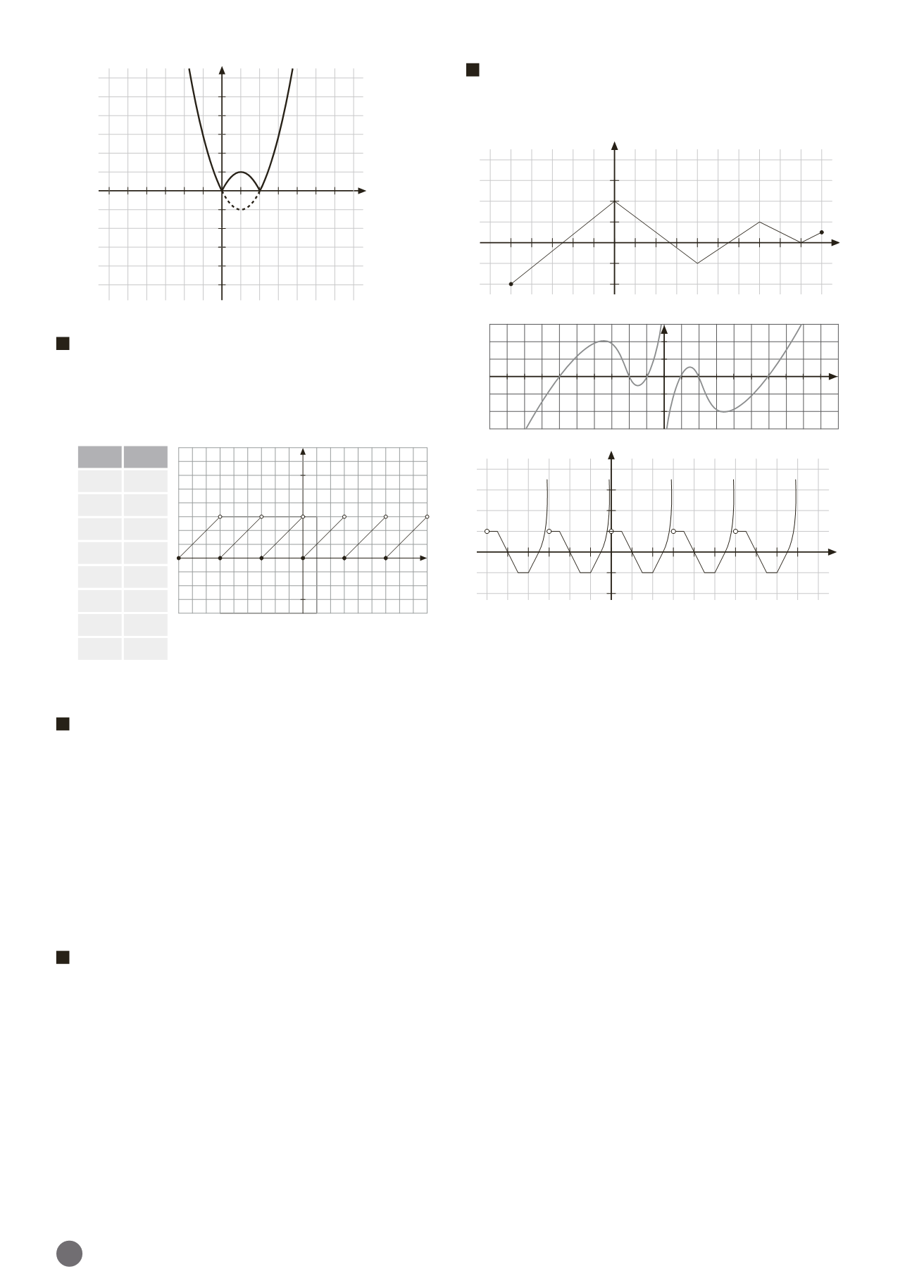
Estudia en las funciones que muestran las figuras, los inter-
valos de signo constante, la monotonía y la curvatura si es
posible. ¿Está acotada alguna de las funciones? ¿Hay algu-
na que presente simetría? ¿Y periodicidad?
F
IGURA
8.57.a.
F
IGURA
8.57.b.
F
IGURA
8.57.c.
Figura 8.57.a.
Intervalos de signo constante:
f
(
x
) 0 en ( 2,5, 2,5)
(5,5, 9)
(9, 10]
f
(
x
) 0 en [ 5,
2,5)
(2,5, 5,5)
f
(
x
) es estrictamente creciente en ( 5, 0), en (4, 7) y en
(9, 10).
f
(
x
) es estrictamente decreciente en (0, 4) y en (7, 9).
Función acotada,
⏐
f
(
x
)
⏐
2, no es simétrica ni periódica.
Figura 8.57.b.
Intervalos de signo constante:
f
(
x
) 0 en ( 6,
2)
( 1, 0)
(1, 2)
(6,
∞
)
f
(
x
) 0 en (
∞
,
6)
( 2,
1)
(0, 1)
(2, 6)
f
(
x
) es estrictamente creciente en (
∞
, 3,5), en ( 1,5, 0) ,
en (0, 1,5) , y en (3,5,
∞
).
f
(
x
) es estrictamente decreciente en ( 3,5;
1,5), y en
(1,5; 3,5).
Es convexa en (
∞
,
3)
(0; 2,5) y cóncava en
( 3, 0) (2,5;
∞
).
Es una función no acotada, sí es simétrica respecto al ori-
gen de coordenadas, y por tanto, impar, y tampoco es pe-
riódica.
Figura 8.57.c.
Intervalos de signo constante:
Dado que es una función periódica de período
T
3:
f
(
x
) 0 en (0 3
k
, 1 3
k
) (2,5 3
k
, 3 3
k
) , para todo
k
.
f
(
x
) 0 en (1 3
k
, 2,5 3
k
), para todo
k
.
f
(
x
) es estrictamente creciente en (2 3
k
, 3 3
k
),
k
.
f
(
x
) es estrictamente decreciente en (0,5 3
k
, 1,5 3
k
),
k
.
f
(
x
) es constante en (0 3
k
, 0,5 3
k
) en (1,5 3
k
, 2 3
k
),
para todo
k
.
Es cóncava en (3
k
1, 3
k
) para todo
k
.
Es una función no acotada.
Y
X
O
3
2
1
2
1 2 3 4 5 6 7
1 2 3 4 5
8 9
1
2
O
X
1 2 3 4
Y
5 6 7 8 9
2
2 4 6 8
Y
X
O
3
1
2
1
2
2 3 4 5 6 7 8 9
1 2 3 4 5
33
x
f
(
x
)
0
0
1
0
1,5
0,5
1,75
0,75
0,5
1,5
1
1,75
0,5
0,5
0
0,25


