17
8.
Funciones
Ejercicios de aplicación
Considera las siguientes funciones:
f
(
x
) 2
x
2
3
x
1
g
(
x
)
(
x
1)
2
h
(
x
)
x
2
x
1
i
(x)
3
x
2
x
2
a)
Represéntalas gráficamente, indicando sus ceros, sus vér-
tices y sus ejes de simetría.
b)
Estudia su signo.
c)
Indica sus intervalos de monotonía y sus recorridos.
d)
Escribe las funciones valor absoluto correspondientes a
cada una como funciones a trozos, y represéntalas.
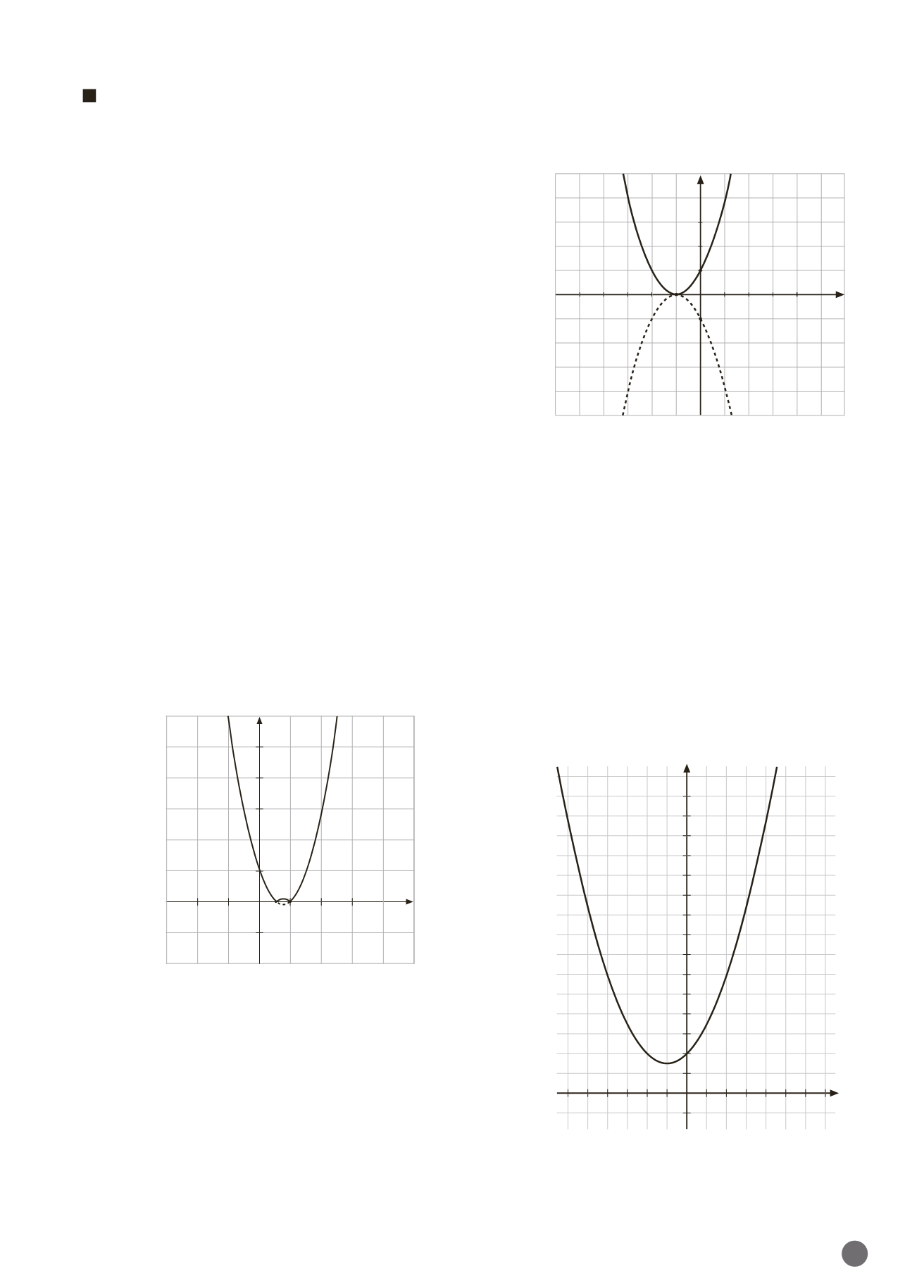
f
(
x
) 2
x
2
3
x
1 es una función polinómica de segundo
grado, con
a
0, por tanto, su representación corresponde
a una parábola con las ramas hacia arriba, y su vértice es el
punto que separa un intervalo de decrecimiento de otro de
crecimiento.
Dado que el vértice es el punto cuya abscisa es:
x
2
a
b
4
3
En
∞
,
4
3
,
f
(
x
) es estrictamente decreciente.
En
4
3
∞
,
f
(
x
) es estrictamente creciente.
Su eje de simetría es la recta
x
4
3
.
Sus ceros son 1 y
1
2
, por lo que
f
(
x
) 0 en
∞
,
1
2
(1,
∞
) y
f
(
x
) 0 en
1
2
, 1 .
Su recorrido es
1
8
,
∞
.
2
x
2
3
x
1 en
∞
,
1
2
[1,
∞
)
⏐
2
x
2
3
x
1
⏐
2
x
2
3
x
1 en
1
2
, 1
g
(
x
)
(
x
1)
2
es una función polinómica de segundo
grado, con
a
0, por tanto, su representación corresponde
a una parábola con la ramas hacia abajo, y su vértice es el
punto que separa un intervalo de crecimiento de otro de
decrecimiento.
Dado que el vértice es el punto cuya abscisa es:
x
2
a
b
1
X
O
Y
1
1
f
(
x
)
2
x
2
3
x
1
3
1
1
2
|
f
(
x
)|
|2
x
2
3
x
1|
48
En (
∞
, 1),
g
(
x
) es estrictamente creciente.
En ( 1,
∞
),
g
(
x
) es estrictamente decreciente.
Su eje de simetría es la recta
x
1.
Tiene un cero, 1, por lo que
g
(
x
) 0 en
{ 1}.
Su recorrido es (
∞
, 0].
h
(
x
)
x
2
x
1 es una función polinómica de segundo
grado, con
a
0, por tanto, su representación correspon-
de a una parábola
con las ramas hacia arriba
, y su vértice
es el punto que separa un intervalo de decrecimiento de
otro de crecimiento.
Dado que el vértice es el punto cuya abscisa es:
x
2
a
b
2
1
En
∞
,
2
1
,
h
(
x
) es estrictamente decreciente.
En
2
1
,
∞
,
h
(
x
) es estrictamente creciente.
Su eje de simetría es la recta
x
2
1
.
No tiene ceros. Es siempre positiva.
Su recorrido es
3
4
,
∞
.
i
(
x
)
3
x
2
x
2 es una función polinómica de segundo
grado, con
a
0, por tanto, su representación corresponde
a una parábola invertida, y su vértice es el punto que sepa-
ra un intervalo de crecimiento de otro de decrecimiento.
X
O
Y
1
1
2
2
1
3
4
3
3
2
5
6
7
h
(
x
)
x
2
x
1
|
h
(
x
)| |
x
2
x
1|
x
2
x
1
g
(
x
)
(
x
1)
2
(
x
1)
2
1
2
3
1 2
-5 -4 -3 -2 -1
-4
-3
-2
-1
g
(
x
)
(
x
1)
2
3
X
Y


