11
8.
Funciones
En el aparcamiento de unos grandes almacenes se debe
abonar 1,50
€
por cada hora o fracción de hora, hasta un
máximo de 12
€
, siendo las dos primeras horas gratuitas.
Representa gráficamente la función que expresa el importe
del aparcamiento en función del tiempo transcurrido.
Se trata de una función escalonada en la que durante las dos
primeras horas hay un valor constante, luego para cada inter-
valo entre una hora y otra toma otro valor constante, hasta
las 9 horas y a partir de ahí es constante de valor 12
€
.
El servicio de correos de un cierto país tiene las siguientes
tarifas para el envío de cartas:
Hasta 20 g de peso, se paga 0,35
€
. Por cada 10 g o fracción
de 10 g de exceso de peso, se añaden 0,07
€
más.
a)
Expresa la relación entre el precio del envío,
y
, y el peso
de la carta,
x,
hasta 50 g.
b)
Representa gráficamente la función.
a)
Se trata de una función definida a trozos:
b)
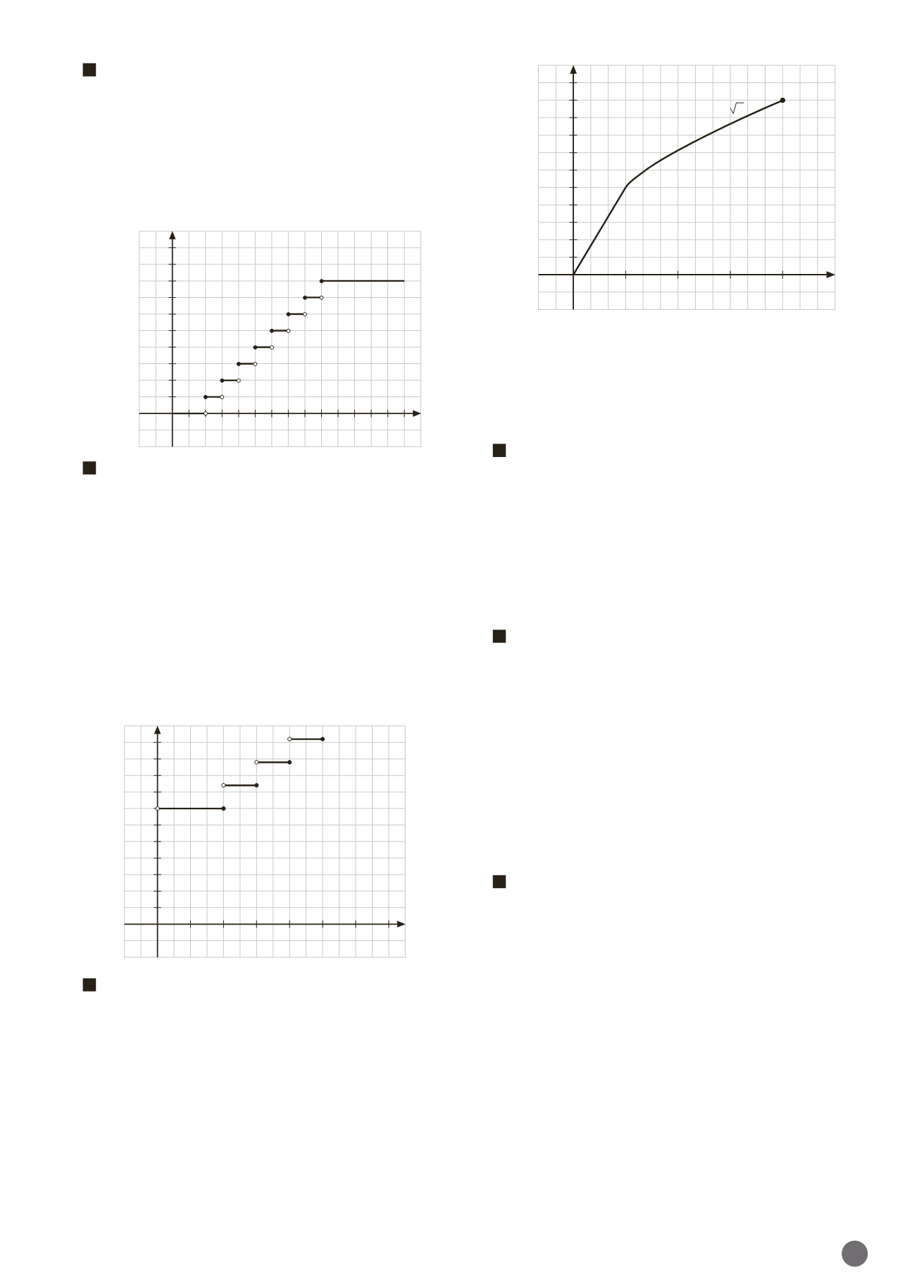
En un concurso, los participantes deben contestar
100 preguntas. En las 25 primeras, se ganan 200
€
por
cada una que se acierte. A partir de aquí, el premio es, en
miles de euros, la raíz cuadrada del número de preguntas
acertadas.
a)
Expresa, mediante una función, la relación entre res-
puestas correctas y cantidad ganada, y represéntala.
b)
¿Cuál es su dominio? ¿Y su recorrido?
c)
¿Cuántas respuestas ha debido acertar un participante
que ha ganado 6 082,76
€
?
a)
200
x
si 0
x
25
f
(
x
)
10
3
x
si 25
x
100
18
0,05
50 60 70
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,45
0,5
peso del paquete (g)
40
30
20
10
0,55
tarifa (
€
)
0,35 si 0
x
20
0,42 si 20
x
30
f
(
x
)
0,49 si 30
x
40
0,56 si 40
x
50
17
1
1,50
2 3 4 5 6 7 8 9 10 11 12 13 14
3
4,50
6
7,50
9
10,50
12
13,50
15
horas transcurridas
importe del aparcamiento (
€
)
16
b)
Su dominio es el conjunto de enteros no negativos,
n
, tal
que 0
n
100.
Su recorrido está formado por los números
n
enteros no
negativos, 200
n
, si 0
n
25 y el conjunto de números
1 000
n
si 25
n
100.
c)
Si ha ganado 6 082,76
€
ha acertado 37 respuestas.
Una lancha circula, cuando se ha alejado 60 kilómetros del
muelle, a una media de 60 km/h. En ese mismo instante,
desde el muelle sale otra lancha a una velocidad media de
75 km/h. Ambas mantienen la velocidad media constante.
Expresa cómo varía la distancia que las separa en función
del tiempo. Cuando la segunda lancha haya adelantado en
45 km a la primera, ¿qué tiempo habrá transcurrido?
La distancia será:
d
(
t
)
|15
t
60|.
Transcurren 7 horas para que la segunda lancha adelante en
45 km a la primera.
El beneficio mensual de un artesano expresado en euros,
cuando fabrica y vende
x
objetos, se ajusta a la función
B
(
x
)
0,5
x
2
50
x
800, donde 20
x
60.
a)
Determina el beneficio que obtiene cuando fabrica y
vende 20 objetos y 60 objetos, respectivamente.
b)
¿Cuántos objetos debe fabricar y vender para obtener el
máximo beneficio?, ¿a cuánto asciende?
a)
B
(20)
0
€
;
B
(60)
400
€
b)
La función beneficio tiene su valor máximo en
x
2
b
a
50
1
50, es decir, cuando fabrica y vende 50 objetos
su beneficio es máximo y es de
B
(50)
450
€
.
Si el precio de la entrada al cine es de 6
€
, van 320 perso-
nas. Se sabe que si aumenta el precio en 0,25
€
, hay 10 es-
pectadores menos. Halla:
a)
La función que determina el número de espectadores
en función del precio de la entrada.
b)
La función que determina los ingresos del cine en fun-
ción del precio de la entrada.
c)
El precio de la entrada para obtener el máximo ingreso.
a)
La función es una recta que pasa por el punto (6, 320) y
tiene pendiente
0
1
,2
0
5
40, por tanto, siendo
e
el nú-
mero de espectadores y
x
el precio de la entrada:
e
(
x
)
320
40(
x
6)
560
40
x
b)
Multiplicando espectadores por precio:
I
(
x
)
560
x
40
x
2
c)
I
(
x
) es una función polinómica de segundo grado, con un
máximo en
x
56
8
0
0
7
€
, es decir, los ingresos son má-
ximos cuando el precio de la entrada es de 7
€
.
21
20
19
1000
100
número de respuestas correctas
75
50
25
2000
3000
4000
5000
6000
7000
8000
9000
10000
11000
y
= 200
x
y
= 1000
x
cantidad ganada (
€
)


