10
Análisis
En la siguiente tabla se detalla el ahorro que se produce en
el intercambio de bombillas, en función de la diferencia de
potencia que consumen:
¿Qué tipo de función relaciona el ahorro,
A,
con la diferen-
cia de potencia consumida,
D
?
La relación es directamente proporcional. Es una función li-
neal. Se observa que:
2
4
0
6
3
,
3
6 9
4
,
9
8
. . .
0,2
El ahorro que se estima por vatio de potencia consumida es de
0,20
€
, por tanto, por un kilovatio será de 200
€
.
La longitud de una varilla de metal varía en función de la
temperatura a la que se somete. La tabla muestra la rela-
ción entre la temperatura y la longitud de dicha varilla, que
inicialmente está a 20 °C y mide 35 m de longitud:
Sabiendo que la relación entre la longitud de la varilla y el
incremento de temperatura es afín, halla la expresión analí-
tica
L
(
t
). ¿Cuánto medirá la varilla a 80 °C?
La relación es lineal:
l
(
t
)
at b
Sustituyendo los datos que proporciona la tabla, se puede
obtener y comprobar que:
l
(
t
) 0,0588
t
3 498,824
l
(80) 3 503,528 cm
La varilla a 80 °C medirá 3 503,528 cm.
La facturación que hace una compañía eléctrica cada dos
meses a uno de sus usuarios engloba tres conceptos:
Facturación de la potencia:
por cada kW contratado y por
cada mes, la tarifa es de 2,82
€
.
Consumo:
por cada kWh consumido, la tarifa es de 0,16
€
.
Concepto fijo:
1,13
€
por mes en concepto de equipo de
medida.
Finalmente, al importe se le aplica un 21% de IVA.
Si llamamos
P
a la potencia contratada y
C
al consumo en
kWh de dos meses, halla la función que proporciona el
importe de la factura bimestral.
a)
¿Cuántas variables engloba?
b)
Calcula el total de una factura para una potencia contra-
tada de 4,4 kW y un consumo bimestral de 271 kWh.
a)
Como son dos meses el concepto fijo será 2 1,13 y la fac-
turación de la potencia 2 2,82
P
. Hay que aplicar el IVA
para saber cuánto se paga realmente:
I
(2 2,82
P
0,16
C
2 1,13) 1,21
Esta función engloba dos variables,
P
y
C
.
b)
El usuario que tiene contratada una potencia de 4,4 kW y
un consumo bimestral de 271 kWh, debe pagar a la com-
pañía eléctrica:
I
(2 2,82 4,4 0,16 271 2 1,13) 1,21 85,23
€
13
12
11
Una empresa realiza un estudio comparativo sobre el coste
que suponen dos piezas distintas. Estima que el coste en
euros de la pieza tipo A, en función del número de miles de
piezas,
x,
si el pedido no sobrepasa las 2 000 piezas, viene
dado por la expresión:
C
A
(
x
)
2
x
2
5
x
Y el coste de la pieza tipo B en las mismas condiciones es:
C
B
(
x
) 2
x
2
3
x
2
a)
¿Para qué número de piezas es menor el coste de la pro-
ducción de la pieza tipo A?
b)
Para un pedido de 2 000 piezas, ¿qué tipo de pieza
produce menor coste a la empresa?
c)
¿Cuántas piezas del tipo B producen menor coste?
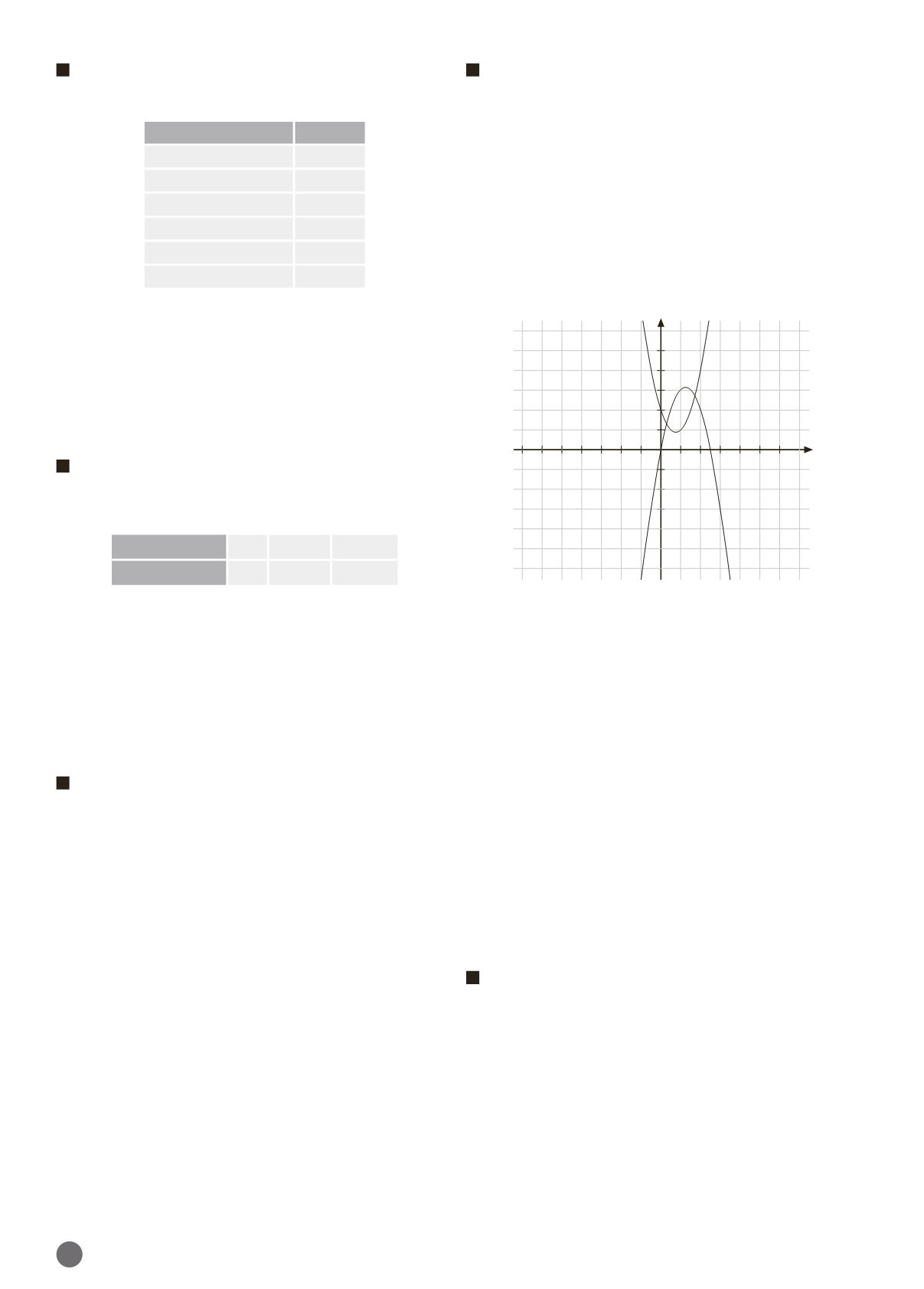
Debemos calcular los puntos de intersección de las dos gráfi-
cas, es decir, el número de piezas de un tipo u otro que pro-
ducen a la empresa el mismo coste:
C
A
(
x
)
C
B
(
x
) si 2
x
2
5
x
2
x
2
3
x
2
⇒
⇒
4
x
2
8
x
2
0
⇒
2
x
2
4
x
1 0
Resolviendo obtenemos:
x
0,293 y
x
1,707
Como
x
viene dado en miles de piezas, la solución será 293
piezas y 1 707 piezas.
a)
La pieza tipo A tiene menor coste para un pedido menor
de 293 unidades o para un pedido de entre 1 707 y 2 000
unidades (el enunciado especifica que el pedido no sobre-
pase las 2 000 piezas).
b)
Para un pedido de 2 000 piezas es menor el coste de la pie-
za tipo A, ya que si observamos en la gráfica el valor de
x
2 para las dos funciones, es menor en la función tipo A.
c)
El mínimo de la función
C
B
(
x
) se produce en el vertice de la
función:
2
b
a
3
4
0,750
⇒
x
750 piezas
Un granjero va cerrar un terreno rectangular de 80 m
2
con
una valla. Uno de los lados linda con la carretera, por lo que
la valla de este lado es más resistente y cuesta 15
€
/m, y el
resto de valla está a 10
€
/m.
Expresa, en función del lado que linda con la carretera,
x,
el
precio total de la valla.
En primer lugar,
xy
80, por lo que
y
8
x
0
.
Los dos lados
y,
y un lado
x
cuestan 10
€
/m y el otro lado
x,
15
€
/m.
Por tanto:
C
(
x
)
x
2
8
x
0
10 15
x
25
x
1 6
x
00
15
X
O
Y
1
2
1
3
1 2 3 4
2 1
3 45 6
2
5 6
4
5
6
3
4
5
7
y
= 2
x
2
5
x
y
= 2
x
2
3
x
2
14
Intercambio de bombillas
Ahorro (
€
)
25 W
→
5 W
4
40 W
→
7 W
6,6
60 W
→
11W
9,8
75 W
→
15 W
12
100 W
→
20 W
16
120 W
→
23 W
19,4
Temperatura (
°
C)
Longitud (cm)
20
3 500
40
3 501,176
60
3 502,352


