16
Análisis
Función inversa
¿Existe función inversa respecto de la composición para las
siguientes funciones? Si es así, halla su expresión.
a)
f
(
x
) 3
x
2
e)
f
(
x
)
4
x
1
2
b)
f
(
x
)
x
4
x
3
f)
f
(
x
)
x
1
x
c)
f
(
x
)
3
x
8
g)
f
(
x
)
x
2
3
x
1
d)
f
(
x
)
x
2
5
x
h)
f
(
x
)
1
4
x
a)
f
(
x
) es biyectiva, por tanto, tiene inversa:
f
1
(
x
)
x
3
2
b)
f
(
x
) es inyectiva:
f
1
(
x
)
4
x
3
1
c)
f
1
(
x
)
x
3
8
e)
f
(
x
) es inyectiva:
f
1
(
x
)
1
4
x
2
x
h)
f
1
(
x
)
x
4
1
Las funciones de los apartados
d), f )
y
g)
no son inyectivas y
por tanto no existe su función inversa.
Representa la función
f
(
x
)
x
1 y su inversa.
Transformaciones de funciones
A partir de la función
f
(
x
)
1
x
, representa las siguientes fun-
ciones e indica sus dominios y recorridos:
a)
f
(
x
)
x
1
2
b)
f
(
x
) 2
x
1
2
c)
f
(
x
)
3
1
x
a)
Dom
f
{2}
Rec
f
{0}
X
O
Y
1
2
1
1 2 3 4
2 1
3 45 6
5 6
3
4
5
3
2
4
5
y
=
x
2
1
46
Y
X
1
1
y
x
f
(
x
)
x
1
O
f
1
(
x
)
x
1
45
44
b)
Dom
f
{2}
Rec
f
{2}
c)
Dom
f
0
Rec
f
0
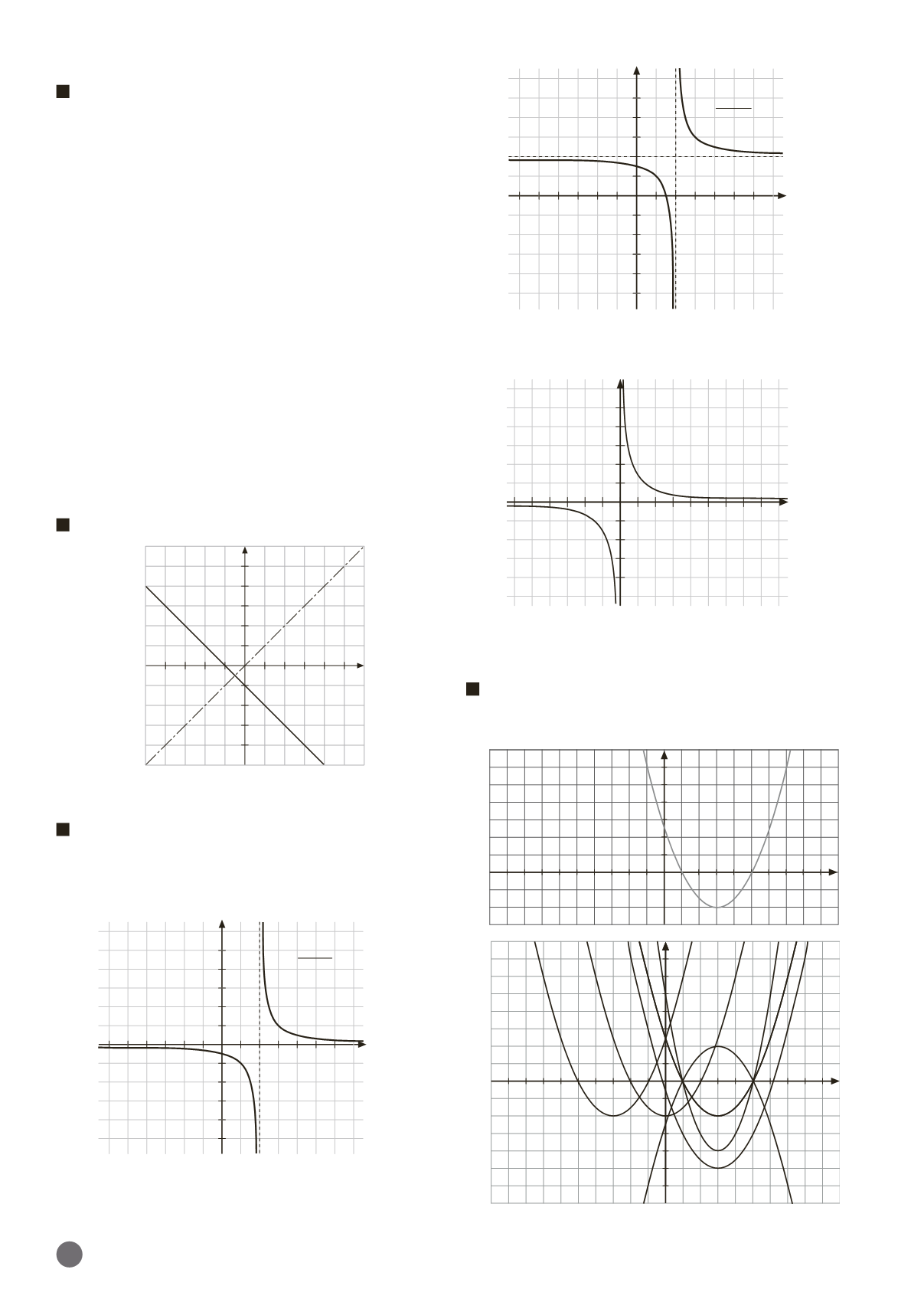
A partir de la gráfica de la función
f
(
x
) de la figura, repre-
senta:
f
(
x
),
f
(
x
),
f
(
x
3),
f
(
x
) 3 y 2
f
(
x
)
X
O
Y
1
1
2
· f
(
x
)
f
(
x
) 3
f
(
x
)
f
(
x
)
f
(
x
)
f
(
x
3)
O
X
Y
5
5
5
47
1 1
X
Y
2
3
4
2 3 4 5 6 7
23456
1
2
3
4
5
8
f
(
x
)
---------1
3
x
X
O
Y
1
2
1
1 2 3 4
2 1
3 45 6
5 6
3
4
5
3
2
4
5
y
= 2
x
2
1


