9
11
Funciones
11
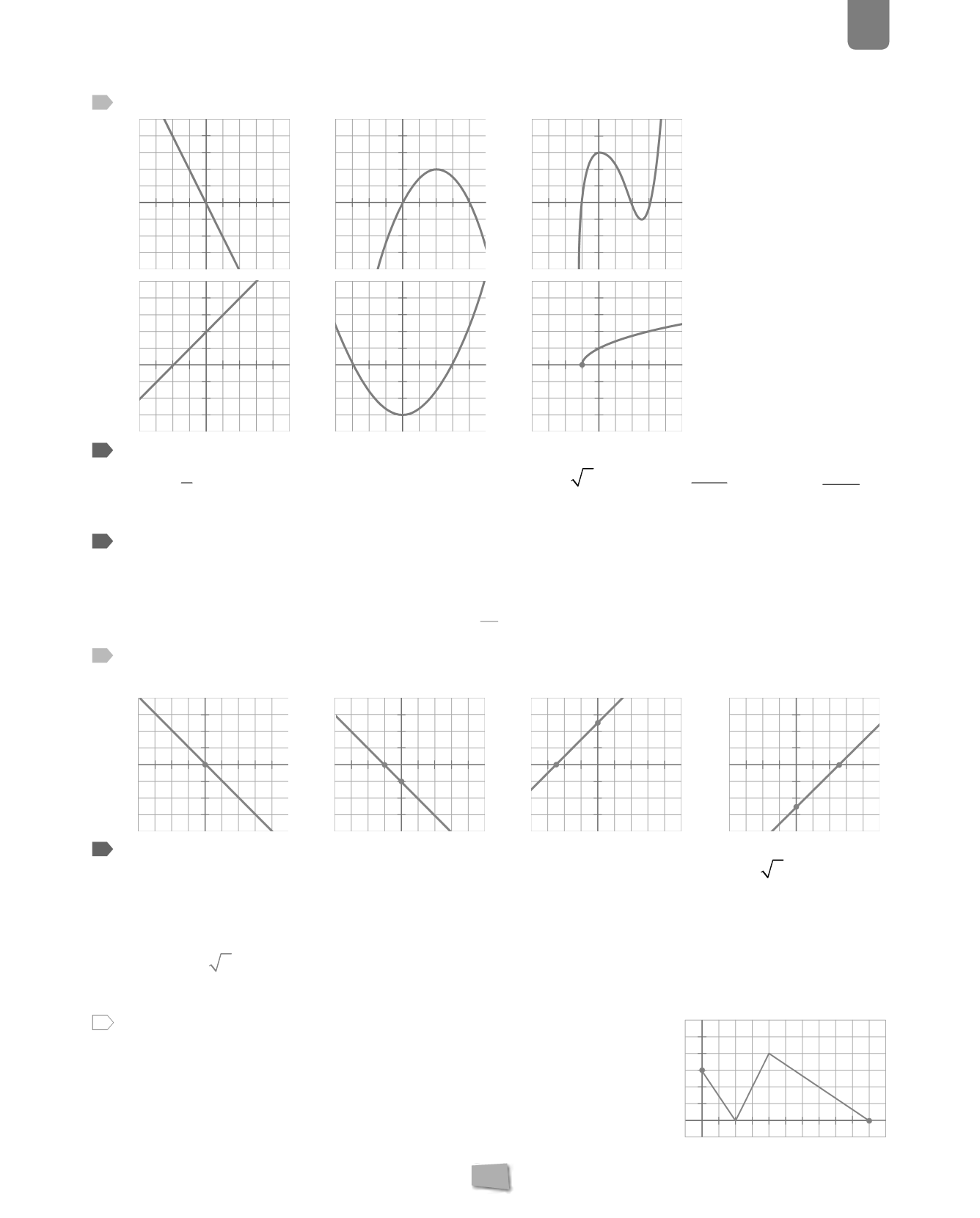
Estudia el dominio, el recorrido y los puntos de corte con los ejes de estas funciones.
a)
c)
e)
O
1
1
X
Y
O
1
1
X
Y
O
1
1
X
Y
b)
d)
f)
O
1
1
X
Y
O
1
1
Y
X
O
1
1
Y
X
12
Halla algebraicamente el dominio de:
a)
f
(
x
)
=
1
x
b)
f
(
x
)
=
x
2
−
5
x
+
6
c)
f
(
x
)
=
x
2
+
x
d)
f
(
x
)
=
x
e)
f
(
x
)
=
x
x
+
2
f)
f
(
x
)
=
x
+
1
x
−
5
a)
Dom
f
=
R
−
{0}
b)
Dom
f
=
R
c)
Dom
f
=
R
d)
Dom
f
=
[0,
+
∞
)
e)
Dom
f
=
R
−
{
−
2}
f)
Dom
f
=
R
−
{5}
13
La superficie de un rectángulo mide 18 cm
2
.
a)
Expresa algebraicamente la relación entre las variables
base
y
altura del rectángulo.
b)
Estudia el dominio de la función dada por la expresión que has escrito en el apartado anterior.
a)
Si
b
es la base y
a
la altura, resulta:
b
⋅
a
=
18
→
b
=
18
a
b)
Dominio
=
(0,
+
∞
)
14
Calcula los puntos de corte con los ejes de las siguientes funciones y utilízalos para dibujarlas.
a)
y
=
−
x
b)
y
=
−
x
−
1
c)
y
=
x
+
5
d)
y
=
x
−
5
a)
b)
c)
d)
O
Y
X
1
1
O
Y
X
1
1
O
Y
X
2
2
O
Y
X
2
2
15
Calcula los puntos de corte con los ejes de estas funciones.
a)
y
=
2
x
2
−
2
b)
y
=
x
2
−
1
c)
y
=
−
x
2
+
3
x
d)
y
=
x
a)
Cortes con eje
X
: 2
x
2
−
2
=
0
x
=
1 y
x
=
−
1
(
−
1, 0) y (1, 0). Corte con eje
Y
: Si
x
=
0
y
=
−
2
(0,
−
2)
b)
Con eje
X
:
x
2
−
1
=
0
x
=
1 y
x
=
−
1
(
−
1, 0) y (1, 0). Con eje
Y
: Si
x
=
0
y
=
−
1
(0,
−
1)
c)
Con eje
X
:
−
x
2
+
3
x
=
0
x
(
−
x
+
3)
=
0
x
=
0 y
x
=
3
(0, 0) y (3, 0). Con eje
Y
: Si
x
=
0
y
=
0 (0, 0)
d)
Con eje
X
:
x
=
0
x
=
0 (0, 0). Con eje
Y
: Si
x
=
0
y
=
0 (0, 0)
Desafío
16
Dibuja la gráfica de una función que verifique lo siguiente.
❚
Su dominio es el intervalo [0, 10] y su recorrido es el intervalo [0, 4].
❚
f
(4)
=
4
❚
Los puntos de corte con el eje
X
son: (2, 0) y (10, 0)
❚
Corta al eje
Y
en el punto: (0, 3)
a)
Dom y Rec:
R
Corte: (0, 0)
b)
Dom
f
=
R
Recorrido
=
R
Corte: (
−
2, 0) y (0, 2)
c)
Dom
f
=
R
Recorrido
=
(
−∞
, 2]
Corte: (0, 0) y (4, 0)
d)
Dom
f
=
R
Recorrido
=
[
−
3,
+
∞
)
Corte: (
−
3, 0), (3, 0) y
(0,
−
3)
e)
Dom
f
=
R
Recorrido
=
R
Corte: (
−
1, 0), (2, 0),
(3, 0) y (0, 3)
f)
Dom
f
=
[
−
1,
+
∞
)
Recorrido
=
[0,
+
∞
)
Corte: (0, 0) y (0, 1)
O
Y
X
1
1


