13
11
Funciones
23
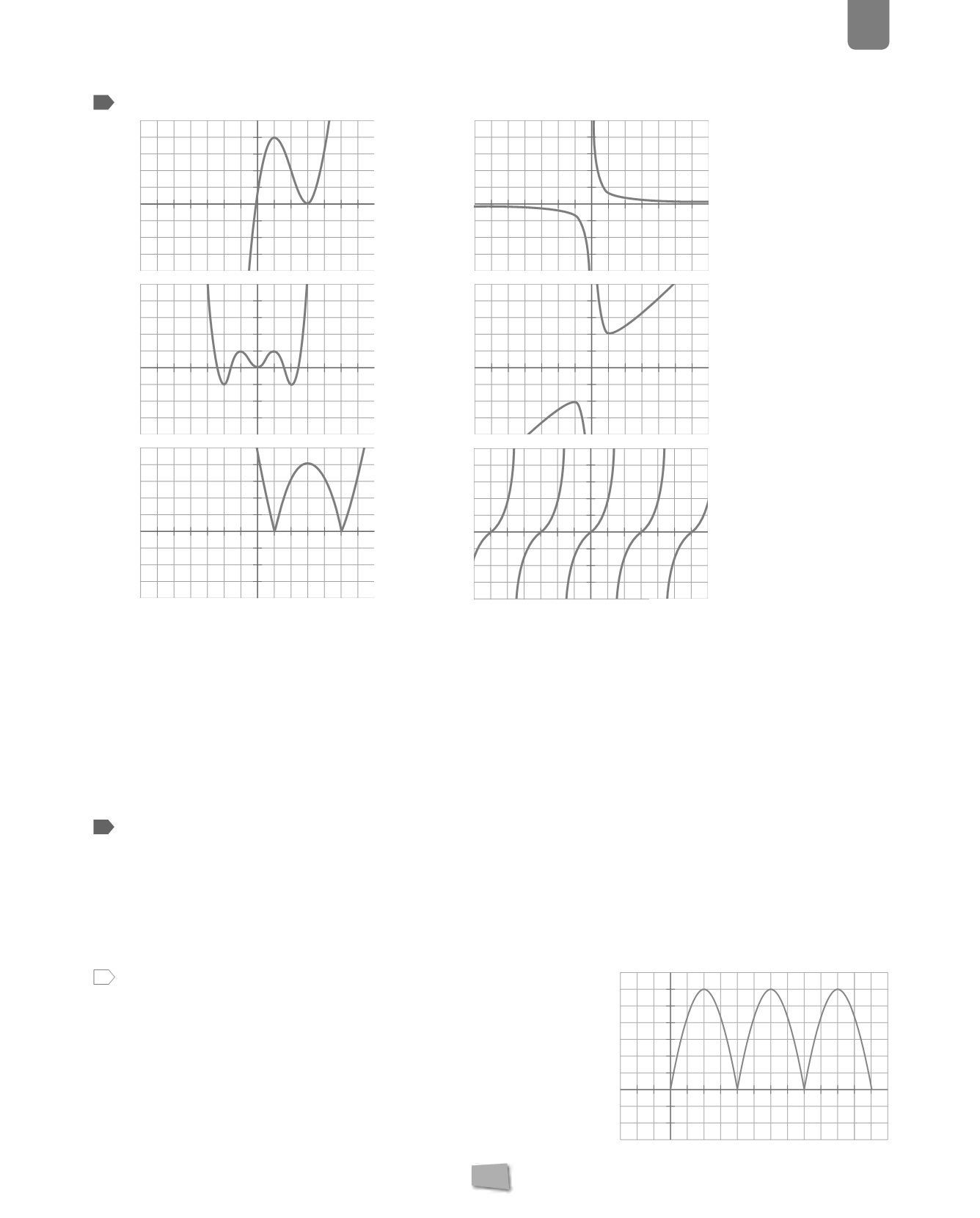
Indica los intervalos de crecimiento y decrecimiento de estas funciones, así como sus máximos y mínimos.
a)
d)
O
1
1
X
Y
O
1
1
X
Y
b)
e)
O
1
1
X
Y
O
1
1
X
Y
c)
f)
O
1
1
X
Y
O
1
1
X
Y
a)
Es creciente en (
−∞
, 1) y (3,
+
∞
) y es decreciente en el intervalo (1, 3).
El punto máximo es (1, 4) y el punto mínimo, (3, 0).
b)
Es creciente en (
−
2,
−
1), (0, 1) y (2,
+
∞
), es decreciente en (
−∞
,
−
2), (
−
1, 0) y (1, 2).
Los puntos máximos son (
−
1, 1) y (1, 1), los puntos mínimos, (
−
2,
−
1), (0, 0) y (2,
−
1).
c)
Es creciente en (1, 3) y (5,
+
∞
) y es decreciente en (
−∞
, 1) y (3, 5).
El punto máximo es (3, 4) y los puntos mínimos, (1, 0) y (5, 0).
d)
Es decreciente en todo su dominio. No tiene puntos máximos ni mínimos.
e)
Es creciente en (
−∞
,
−
1) y (1,
+
∞
), es decreciente en (
−
1, 0) y (0, 1). El máximo es (
−
1,
−
2), y el punto mínimo, (1, 2).
f)
Es creciente en todo su dominio. No tiene puntos máximos ni mínimos.
24
Razona si estas afirmaciones son verdaderas o falsas.
a)
Hay funciones que no tienen máximos ni mínimos.
b)
Entre dos puntos mínimos necesariamente hay dos puntos máximos.
a)
Verdadera, por ejemplo
y
=
x
es creciente en todo su dominio.
b)
Falsa, entre dos puntos mínimos, en una función continua, hay solo un punto máximo.
Desafío
25
Dibuja aproximadamente la gráfica de la función que describe la altura de
una de las cabinas de una noria de 70 m de altura. Estudia la monotonía de
esta función.
Es una función creciente en los intervalos: (0, 30), (60, 90) y (120, 150)
Es decreciente en los intervalos: (30, 60), (90, 120) y (150, 180)
Altura
Tiempo
O
10
15


