8
Análisis
Calcula la función inversa,
f
1
(
x
), de las siguientes fun-
ciones:
a)
f
(
x
)
1
6
3
x
b)
f
(
x
)
2
3
2
x
c)
f
(
x
)
7
x
x
d)
f
(
x
)
3
x
2
e)
f
(
x
)
4
3
5
x
x
a)
f
1
(
x
)
1
3
6
x
b)
f
1
(
x
)
2
x
2
x
3
c)
f
1
(
x
)
1
7
x
d)
f
1
(
x
)
x
3
2
e)
f
1
(
x
)
3
5
x
4
1
x
A partir de la gráfica de
f
(
x
), identifica las funciones repre-
sentadas.
g
(
x
)
f
(
x
)
4;
h
(
x
)
f
(
x
);
i
(
x
)
f
(
x
5)
Ejercicios y problemas
(páginas 230/234)
)
Funciones. Modelización
Averigua la función que permite obtener el volumen de un
cubo en función de su diagonal,
d.
Siendo
x
la arista del cubo, su volumen es
V x
3
.
Como la diagonal de un cubo,
d
, es, en función de la arista,
d x
3, se obtiene que el volumen de un cubo, en función
de su diagonal:
V
d
3
9
3
En un triángulo isósceles se
inscribe un rectángulo como se
muestra en la figura 8.49. Halla
la función que proporciona la
superficie del rectángulo en
función de su base,
b.
¿Cuál es
el dominio de esta función? ¿Y
su recorrido?
De la semejanza de triángulos se puede obtener la siguiente
proporción:
, de donde
h
6
A
(
b
)
b
6
6
b
Función polinómica de grado 2. Para
b
4,
S
(
b
) 12, que corres-
ponde a la superficie máxima que puede tener el rectángulo.
Por lo tanto, Dom
A
(0, 8), Rec
A
(0, 12]
3
b
2
4
3
b
4
3
b
4
6
h
b
6
8
2
d
3
3 3
1
2
4
O
X
2 4 6 8 10
4 8
4
6
Y
h
(
x
)
i
(
x
)
f
(
x
)
g
(
x
)
19
18
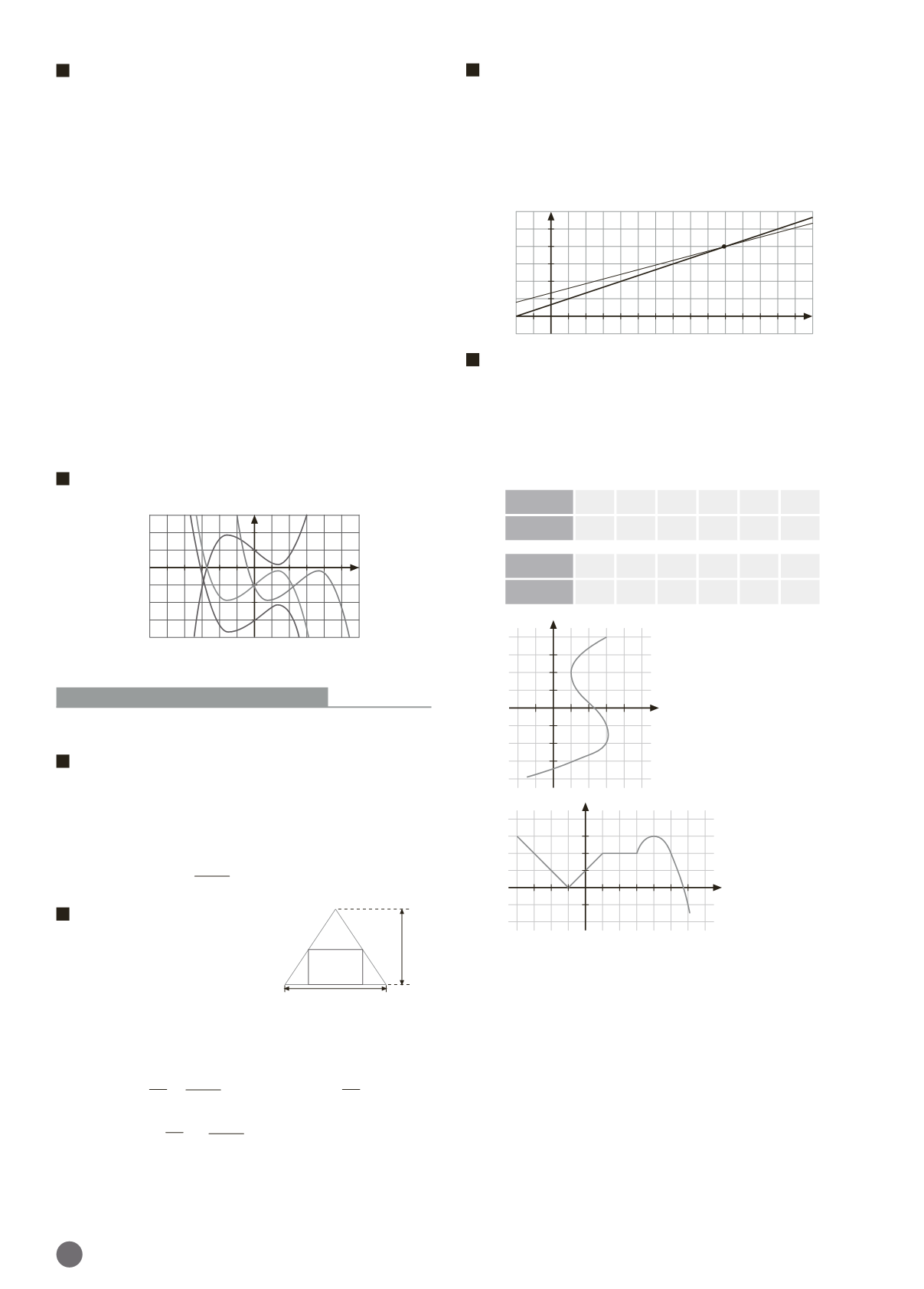
Queremos alquilar un apartamento en verano. Una agen-
cia, A, pide 200
€
de entrada por costes diversos y 40
€
diarios. Otra agencia, B, pide 100
€
de entrada y 50
€
dia-
rios. Dibuja en un mismo sistema de referencia las gráficas
que representan el precio del apartamento en función de
los días, y determina a partir de cuántos días de alquiler re-
sulta más económica la oferta de la agencia A.
A partir de los 10 días.
De entre las siguientes relaciones entre variables que sean
funciones indica el dominio y recorrido:
a)
A todo número real,
x,
se le asigna su inverso.
b)
A cada número real,
x,
se le asigna un número entero,
z,
tal que 0
x z
1.
c)
A cada número real,
x,
se le asigna otro número real,
y
,
de tal manera que se cumpla
x
2
y
2
4.
d)
e)
f)
g)
a)
Es una función. Su dominio y recorrido es
{0}.
b)
Es una función que se denomina parte entera de
x
,
E
(
x
). Su
dominio son todos los reales, y su recorrido los enteros.
c)
No corresponde a una función.
d)
La tabla corresponde a una función constante. Como no
se dan más indicaciones, hemos de suponer que es una
función de dominio discreto.
f
(
x
) 5, Dom
f
{
z
|
2
z
3}, Rec
f
{5}
e)
La tabla no corresponde a una función: para un mismo va-
lor de
x
existen varias imágenes posibles.
f)
La gráfica no corresponde a una función: para un mismo va-
lor de
x
existen varias imágenes posibles.
g)
La gráfica corresponde a una función. Su dominio es
(
∞
,
∞
). Su recorrido es (
∞
,
∞
).
Y
X
3
1 2 3 4 5 6
123
2
1
O
Y
X
3
1
f
(
x
)
2
1
1
2
3
2 3 4
O
4
O
150
1
y
200
40
x
y
100
50
x
(10, 600)
precio (
€
)
n.º de días de alquiler
3
x
y
2
5
1
5
0
5
1
2
3
5
5
5
x
y
3
10
3
7
3
4
3
3
3
1
2
5
b
8 cm
6 cm


