9
8.
Funciones
Un fabricante de latas de refresco necesita producir latas
cilíndricas de 33 cm
3
de volumen. Expresa:
a)
La relación entre la altura de la lata y el radio de su base.
b)
El área total de la lata en función del radio de la base.
a)
V r
2
h
, por tanto, la relación entre la altura y el radio es:
h
b)
A
2
r
2
2
rh
Así, el área de la lata es:
A
2
r
2
2
π
r
2
r
2
Averigua la función que relaciona el área de un rectángulo
con uno de sus lados, sabiendo que su perímetro mide
12 cm. ¿Qué tipo de función es? Represéntala. Halla su
dominio y su recorrido. ¿Para qué valores es creciente?
Suponemos un rectángulo de lados
a
y
b
, por lo tanto:
a b
6
Como
A a b
:
A
(
b
) (6
b
)
b b
2
6
b
Es una función cuadrática.
Su dominio es (0, 6).
Su recorrido es (0, 9].
Es una función creciente
b
(0, 3).
Un centro de estudios alquila un autocar de 60 plazas para
realizar una excursión. El alquiler es de 900
€
. Por cada
alumno que asista, la asociación de padres de la escuela
subvenciona la salida con 2,50
€
. El número mínimo de
asistentes a la salida es de 25 alumnos. ¿Qué función rela-
ciona el precio de la excursión por alumno con el número
de alumnos que asistan? Realiza una gráfica que muestre
esa relación y determina el dominio de dicha función.
La función que proporciona el coste por alumno, siendo
25
x
60 su dominio, es:
C
(
x
)
90
x
0
2,5
4
50 55 60 65 70
8
12
16
20
24
28
32
36
40
coste (
€
)
número de alumnos
45 40 35 30 25 20 15 10 5
7
1
6
1
b
(cm)
A
(cm
2
)
6
66
r
33
r
2
33
r
2
5
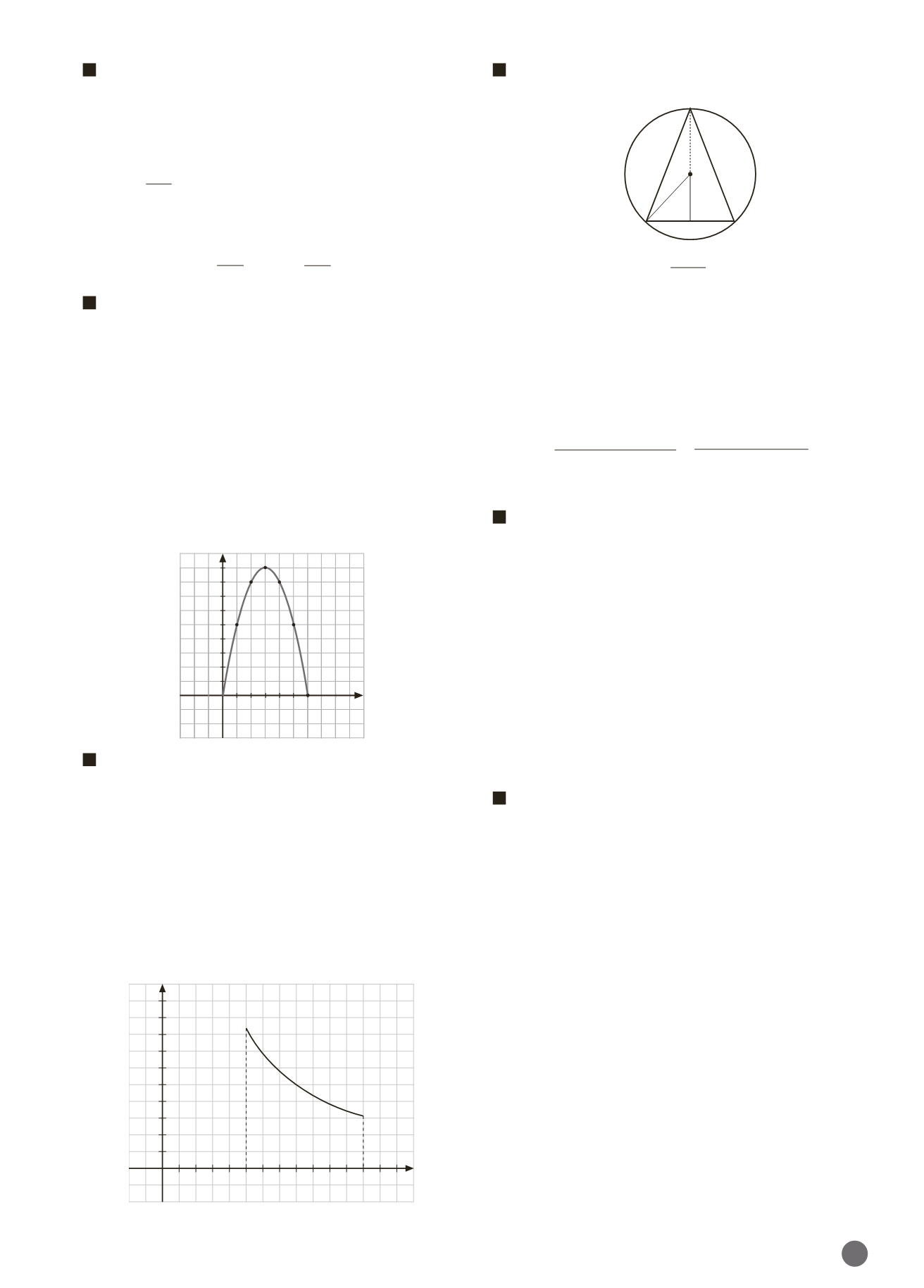
En un círculo de 5 cm de radio se inscribe un triángulo isós-
celes. Halla su área en función de su base,
b.
El área de un triángulo es:
Según muestra la figura, la altura del triángulo,
h
, se puede
descomponer como
h r a
, siendo
a
:
a
r
2
b
2
2
Puesto que el radio vale 5 cm, tenemos que:
A
(
b
)
El dominio de
A
es (0, 10].
Halla la expresión que pasa grados centígrados:
a)
A grados Kelvin, sabiendo que 0 K corresponden a
273 °C, y 373 K, a 100 °C.
b)
A grados Fahrenheit, sabiendo que 32 °F corresponden a
0 °C, y 212 °F, a 100 °C.
a)
Si
x
corresponde a los grados centígrados que se desean
transformar y
K
a sus equivalentes en grados kelvin, tene-
mos que:
K x
273
b)
Si
x
corresponde a los grados centígrados que se desean
transformar y
F
a sus equivalentes en Farenheit, tenemos
que:
F
32
1
1
8
0
0
0
x
32
9
5
x
La cantidad de calor que hay que suministrar a un gramo
de una sustancia para que esta aumente 1°C se llama calor
específico. Sabiendo que cuando se suministran 3 calorías
a un gramo de cinc a 20 °C, la temperatura sube a 52,43 °C,
averigua su calor específico y escribe una función que pro-
porcione el incremento de temperatura de una masa cual-
quiera de cinc en función del aporte de calor.
Dado que se trata de un gramo de sustancia, dividiendo el
calor entre el incremento de temperatura se obtiene el calor
específico del cinc:
32
3
, 4
c
3
al
°C
0,0925 cal/°C
Mediante la definición de calor específico,
c
e
, se puede dedu-
cir que
c
e
calor/(masa incremento de temperatura).
Llamando
Q
al calor suministrado, y despejando de la fórmu-
la anterior el incremento de temperatura,
t
, que se produce
para un gramo de cinc es:
t
0,0
Q
925
10,81
Q
Para una masa de cinc cualquiera,
m:
t
10,
m
81
Q
10
9
b
5 25
b
4
2
2
b r
r
2
b
2
2
2
b h
2
b
5 cm
a
r
8


