233
Movimientos en una y dos dimensiones
2.3.
Los movimientos rectilíneos con aceleración
constante en la naturaleza
La Tierra confiere a los cuerpos que se encuentran en su superficie o cerca de
ella una aceleración constante, cuyo valor aproximado es 9,8 m/s
2
y se simboliza
mediante la letra
g
(de «gravedad»). Dicha aceleración se dirige, aproximadamente,
hacia el centro terrestre, y determina la vertical en cualquier lugar de la Tierra.
Por tanto, cualquier movimiento en la superficie terrestre está sometido a aceleración
constante en la dirección vertical. Los
movimientos rectilíneos con aceleración
constante
en la superficie terrestre son la
caída libre
y el
lanzamiento vertical.
La caída libre de los cuerpos: un desafío al sentido común
¿Qué llegará antes al suelo, una pila grande o un folio? Compruébalo. Repite la mis-
ma operación, pero convirtiendo el folio en una bola compacta. ¿Pesa más el folio
ahora? ¿Cuál puede ser entonces el factor distorsionador de la experiencia?
Hace ya cuatro siglos, a Galileo le costó convencer a sus contemporáneos de que, si
no se considerara la resistencia del aire,
todos los cuerpos, independientemente
de su masa, caerían con la misma aceleración
y, por tanto, llegarían a la par al
suelo partiendo de la misma altura. Pasó mucho tiempo hasta que, en 1971, el as-
tronauta de la misión
Apollo XV,
David R. Scott, verificó de modo inapelable dicha
sentencia al dejar caer sobre la superficie lunar (donde no hay atmósfera) un martillo
y una pluma, y comprobar que ambos objetos llegaban al suelo a la vez. Así:
La aceleración que la Tierra (u otro cuerpo celeste, por ejemplo la Luna) comunica
a los cuerpos es independiente de la masa de estos.
Las ecuaciones de la caída libre
Como su nombre indica, una caída libre consiste en abandonar un cuerpo, sin nin-
gún tipo de impulso inicial (
v
0
=
0), a la mera acción de la gravedad (por tanto,
a
=
−
g,
donde el signo negativo solo indica su actuación vertical hacia abajo) desde
una altura inicial
y
0
medida desde el suelo. Aplicando estas condiciones a las ecua-
ciones generales de un movimiento rectilíneo con aceleración constante, obtenemos
las ecuaciones de caída libre:
MRUA
❚❚
Ecuación de posición:
x
=
x
0
±
v
0
t
±
1
2
at
2
❚❚
Ecuación de velocidad:
v
=
v
0
±
at
CAÍDA LIBRE
❚❚
Ecuación de altura:
y
=
y
0
−
1
2
gt
2
❚❚
Ecuación de velocidad:
v
=
−
gt
Condiciones
particulares
posición
x
→
altura
y
v
0
=
0
a
=
−
g
El signo negativo de la velocidad solo indica su sentido de actuación vertical dirigida
hacia abajo. Su valor o módulo será, simplemente,
v
=
gt
.
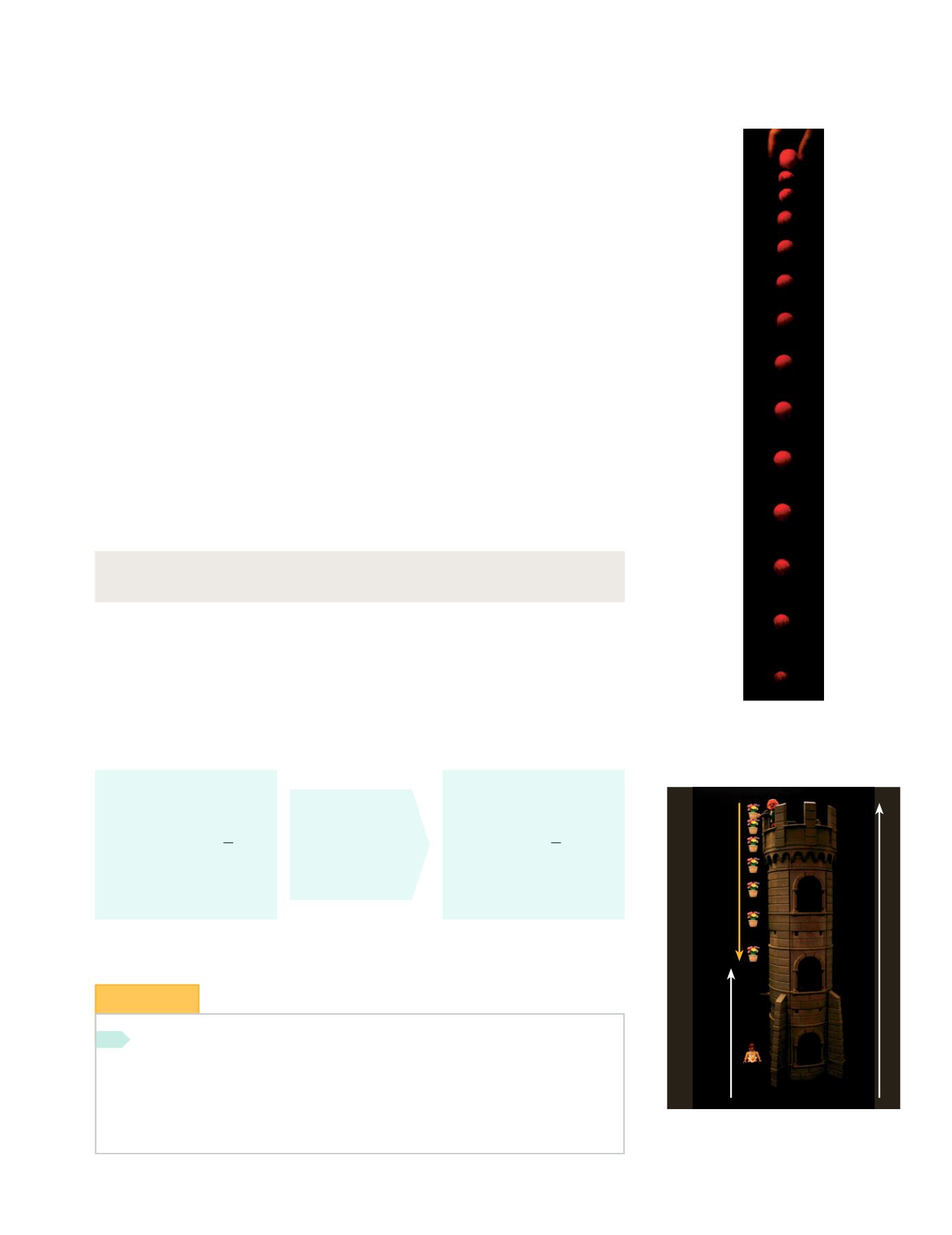
Figura 10.12.
Fotografía estroboscópica de
la caída libre de una pelota.
Actividades
8
En un campeonato de salto de palanca, uno de los participantes se deja
caer a la piscina desde la postura inicial de pino. Si la plataforma está a
10 m de altura:
a)
¿De cuánto tiempo dispone para ejecutar sus piruetas?
b)
¿Con qué velocidad entrará en el agua?
Solución:
a)
1,6 s;
b)
13,7 m/s
Figura 10.13.
Movimiento de caída libre
descrito por el observador que está en el
suelo.
−
1/2
⋅
g
⋅
t
−
2
y
0
y
0


