237
Movimientos en una y dos dimensiones
Observa, en las figuras 10.19 y 10.20, cómo son percibidos los movimientos de caí-
da libre y lanzamiento vertical hacia arriba por el observador O, que se mueve con
velocidad constante, y por el O’, que se halla en reposo en tierra.
Para el observador O, que viaja en la plataforma (figura 10.19), el balón cae libre-
mente en el primer caso y sube y baja verticalmente en el segundo (lanzamiento
vertical).
Sin embargo, para O’, que se halla en reposo en tierra, mientras los balones están
libres en el aire, la plataforma, y con ella el observador O, se ha desplazado cierta
distancia en sentido horizontal (figura 10.20).
Así pues, los dos movimientos de la pelota se describirán como una media parábola,
en el primer caso, y como una parábola completa en el segundo. Fíjate que, en el
caso del observador O’, las parábolas son el resultado de componer un movimiento
rectilíneo uniforme (el de avance) y un movimiento rectilíneo con aceleración cons-
tante (el vertical).
Esto nos da la clave para interpretar los movimientos parabólicos.
Los
movimientos parabólicos
pueden ser tratados como una
composición de
dos movimientos rectilíneos:
uno horizontal con velocidad constante (MRU) y
otro vertical con aceleración constante (MRUA).
El movimiento de media parábola,
lanzamiento horizontal,
puede considerarse
como la composición de un movimiento rectilíneo uniforme de avance horizontal y
un movimiento de caída libre.
El movimiento de parábola completa,
movimiento parabólico,
puede considerarse
como la composición de un movimiento rectilíneo uniforme de avance horizontal y
un lanzamiento vertical hacia arriba.
❚❚
Lanzamiento horizontal
=
MRU (horizontal)
+
caída libre (vertical).
❚❚
Movimiento parabólico completo
=
MRU (horizontal)
+
lanzamiento hacia
arriba (vertical).
El significado físico de la afirmación anterior es de enorme trascendencia, pues supone
que los movimientos de lanzamiento horizontal y de caída libre son físicamente
equivalentes como lo son, a su vez, el movimiento parabólico completo y el lanza-
miento vertical. De esto cabe deducir que:
❚❚
Un cuerpo lanzado horizontalmente y otro que se deja caer
libremente desde la misma altura tardan lo mismo en llegar
al suelo.
❚❚
Dos cuerpos lanzados, uno verticalmente hacia arriba y el otro
parabólicamente, que alcancen la misma altura tardarán lo
mismo en caer al suelo.
❚❚
La independencia de la masa en la caída libre y el lanzamiento
vertical es igualmente válida en los movimientos parabólicos.
La mortífera «dejada» en el tenis, el tiro a canasta, el toque en
balón volea, el salto de longitud, el disparo a balón parado en el
fútbol, el golpe en pelota vasca o los saltos de esquí, entre otros
ejemplos, son movimientos parabólicos. El tratamiento de estos
movimientos es sencillo, puesto que las ecuaciones componentes
ya se conocen: son la del movimiento rectilíneo uniforme y la del
rectilíneo uniformemente acelerado.
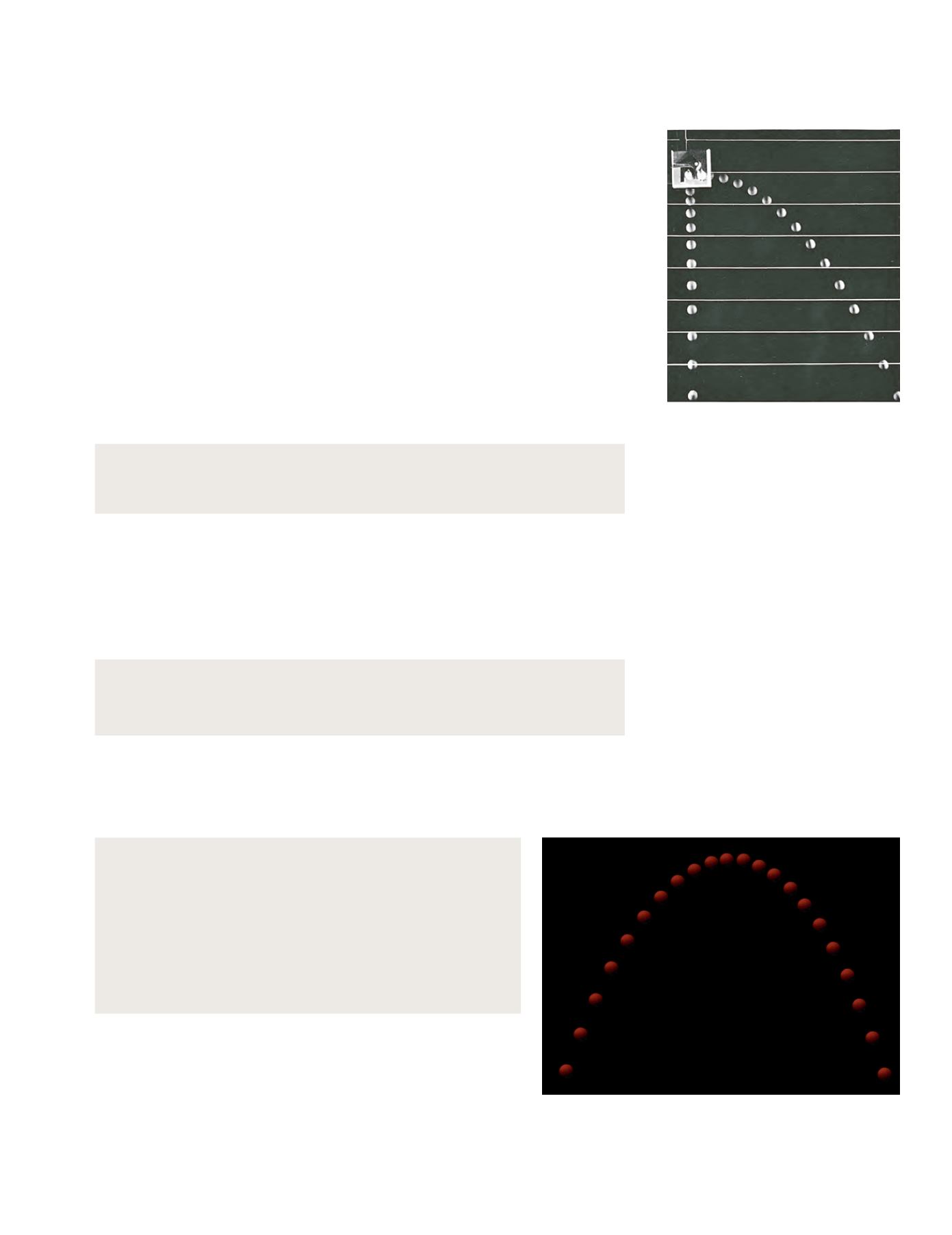
Figura 10.21.
Observa la equivalencia entre
el lanzamiento horizontal de la bola de la
derecha y la caída libre de la situada a la
izquierda. Ambas descienden alturas iguales
en intervalos de tiempo iguales. A su vez, si
mides con una regla te darás cuenta de que
el desplazamiento horizontal de la bola de
la derecha es constante. F
uente
: Uri
H
aber
-S
haim
et al. Física PSSC. Reverté, 1983.
Figura 10.22.
Fotografía estroboscópica de una pelota lanzada
parabólicamente que permite apreciar la perfecta simetría entre
el movimiento de ascenso y el de descenso, al igual que sucedía con
el lanzamiento vertical.


